图论

图论

图论是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。

欧拉回路

前置知识

dfs（深度优先搜索）

深度优先搜索是一种在开发爬虫早期使用较多的方法。它的目的是要达到被搜索结构的叶结点(即那些不包含任何超链的HTML文件) 。在一个HTML文件中，当一个超链被选择后，被链接的HTML文件将执行深度优先搜索，即在搜索其余的超链结果之前必须先完整地搜索单独的一条链。深度优先搜索沿着HTML文件上的超链走到不能再深入为止，然后返回到某一个HTML文件，再继续选择该HTML文件中的其他超链。当不再有其他超链可选择时，说明搜索已经结束。

边权

离散数学或数据结构中，图的每条边上带的一个数值，它代表的含义可以是长度等等，这个值就是边权

欧拉路径

如果图中的一个路径包括每个边恰好一次，则该路径称为欧拉路径。

欧拉回路

首尾相接的欧拉路径称为欧拉回路。

判定

由于每一条边都要经过恰好一次，因此对于除了起点和终点之外的任意一个节点，只要进来，一定要出去。

一个无向图存在欧拉回路，当且仅当该图所有顶点度数都为偶数，且该图只有一个存在边的连通块。

一个无向图存在欧拉路径，当且仅当该图中奇点的数量为0或2，且该图只有一个存在边的连通块。

一个有向图存在欧拉回路，当且仅当所有点的入度等于出度。

一个混合图存在欧拉回路，当且仅当存在一个对所有无向边定向的方案，使得所有点的入度等于出度。需要用网络流。

求法

我们用 dfs来求出一张图的欧拉回路。

我们给每一条边一个 vis数组代表是否访问过，接下来从一个点出发，遍历所有的边。

直接dfs并且记录的话会有一些问题。

为了解决这个问题，我们在记录答案的时候倒着记录，也就是当我们通过 (u, v) 这条边到达 v 的时候，先把 v dfs 完再加入 (v, u) 这条边。

还有一点需要注意。因为一个点可能被访问多次，一不小心可能会写成 O(n ² ) 的（因为每次遍历所有的出边）。解决方案就是设一个cur数组，每次直接从上一次访问到的出边继续遍历。

时间复杂度 O(n + m)。

代码

void dfs(int x)
{
    for(int&hd=head[x];hd;hd=e[hd].nxt)
    {
        if(flag[hd>>1])continue;
        flag[hd>>1]=1;
        dfs(e[hd].to);
        a[++top]=x;
    }
}

拓扑排序

定义

所谓拓扑排序，就是把有向图上的 n 个点重新标号为 1 到 n，满足对于任意一条边 (u, v)，都有 u < v。

并不是所有的图都能进行拓扑排序，只要图中有环，那么就可以导出矛盾。

可以进行拓扑排序的图称为有向无环图（DAG），有很多优美的性质，比如可以在拓扑序上进行 DP（动态规划）。

我们记录一下每一个点的入度和出度，用一个队列维护当前所有入度为 0 的点。 每次拿出来一个入度为 0 的点并且将它加到拓扑序中，然后枚举出边更新度数。 时间复杂度O(n + m)。

（在拓扑排序的过程中可以顺带进行 DP）

代码

    for(int i=1;i<=n;i++)
        if(d[i]==0)q.push(i);
    while(!q.empty())
    {
        int node=q.front();
        q.pop();
        res[++top]=node;
        for(int hd=head[node];hd;hd=e[hd].nxt)
        {
            d[e[hd].to]--;
            if(d[e[hd].to]==0)
                q.push(e[hd].to);
        }
    }

最短路

所谓最短路，就是把边权看做边的长度，从某个点 S到另一个点 T 的最短路径。

用更加数学化的语言描述就是，对于映射 f : V → R，满足 f(S) = 0 且 ∀(x, y, l) ∈ E, |f(x) − f(y)| ≤ l 的情况下，f(T) 的最大值。

单源最短路——Dijkstra

在所有的边权均为正的情况下，我们可以使用 Dijkstra 算 法求出一个点到所有其它点的最短路径。

我们维护一个集合，表示这个集合内的点最短路径已经确定了。

每次我们从剩下的点中选择当前距离最小的点 u 加入这个集合，然后枚举另一个点 v 进行更新：

dv = min(dv, du + w(u, v))

直接这样做时间复杂度是 O(n ² ) 的。

优化

我们注意到，复杂度主要来源于两个地方。

第一个是找出当前距离最小的点。这个可以用堆很容易地实现。

第二个是枚举 v，如果我们用邻接表存图，可以降到边数级别。

这样我们就把复杂度降到了 O((n + m) log n)。

单源最短路——Bellman-Ford

另一种求单源最短路的算法，复杂度不如Dijkstra优秀。

考虑在上面出现过的松弛操作：

dv = min(dv, du + w(u, v))

由于最短路径只会经过最多 n 个点，因此每一个点的最短 路径只会被松弛至多 n − 1 次。

所以我们可以对整张图进行 n − 1 次松弛操作，每次枚举所有的边进行更新。

时间复杂度 O(nm)。

SPFA

它死了。（不要用，它的复杂度是错误的）

应用：费用流

Bellman-Ford 算法不够优秀，于是我们尝试改进这个算法。

注意到，在进行松弛操作的时候，如果点 u 的距离一直没有发生变化，那么就不需要再枚举这个点的出边进行松弛了。

也就是说我们可以用一个队列保存所有距离发生变化的点， 每次取出一个点进行更新。

于是 SPFA就诞生了。

如果图是随机的，SPFA的期望时间复杂度约为 O(2m)，比 之前提到的任何一个算法都优秀，而且还可以有负权。

但是在最坏情况下它的复杂度和 Bellman-Ford 相同，都是 O(nm)，在正式比赛中，没有哪个出题人会放过它。（因为其复杂度本来就是错的）

多源最短路——Floyd

对于一张图，我们希望求出任意两个点之间的最短路径。

我们用 DP（动态规划） 的思想。设 fi,j,k 表示从 i 到 j，途中仅经过前 k个点的最短路。

由于每一个点在最短路中只会出现一次（不然就出现负环了，不存在最短路），所以可以很写出转移方程：

fi,j,k = min(fi,j,k−1, fi,k,k−1 + fk,j,k−1)

时间复杂度是 O(n ³ )。

在实际求的过程中，最后一维可以用滚动数组优化掉，所以空间复杂度是O(n ² )。

代码

for(int k=1;k<=n;k++)

  for(int i=1;i<=n;i++)

    for(int j=1;j<=n;j++)

    dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);

注意三层循环的顺序不能颠倒。

Floyd 传递闭包

有时候，我们需要维护一些有传递性的关系，比如相等，连通等等。（12连通，23连通，则 13连通）

初始条件往往是已知若干个点对具有这些关系，然后让你弄 出来所有的关系。

可以直接把 Floyd 算法做一下调整——

dis[i][j]=dis[i][j]|(dis[i][k]&dis[k][j]);

这个算法叫做传递闭包。

多源最短路——Johnson 重赋权

对于多源最短路，如果我们枚举一个点然后跑堆优化的 Dijkstra，那么复杂度是 O(nm log n) 的，在图比较稀疏的情况下，这个复杂度要优于 Floyd 算法的 O(n ³ )。

但是 Dijkstra 算法要求所有边权均非负。

于是就有了重赋权的技巧。

我们新建一个 0 号点，并且从这个点出发向所有点连一条边 权为 0 的边，然后跑单源最短路。（SPFA 或者 Bellman-Ford）

设距离数组为 h，接下来对于每条边 (u, v)，令 w ′ (u, v) = w(u, v) + h(u) − h(v)。

这样所有的边权就都变成非负了，我们就可以跑 Dijkstra 算法了。

证明

首先由于 h(v) ≤ h(u) + w(u, v)，新图的边权一定非负。

设新图上的最短路径为 d ′，原图上的最短路径为 d。

d ′ (u, v) = min a1,a2,…,ak w ′ (u, a1) + w ′ (a1, a2) + · · · + w ′ (ak, v)

= min a1,a2,…,ak w(u, a1) + (h(u) − h(a1)) + w(a1, a2)+ (h(a2) − h(a1)) + · · · + w(ak, v) + (h(v) − h(ak))

= h(u) − h(v) + min a1,a2,…,ak w(u, a1) + · · · + w(ak, v)

= h(u) − h(v) + d(u, v)

最短路树（最短路图）

所谓最短路树，就是在求完从 S 出发的单源最短路之后，

只保留最短路上的边形成的数据结构。

只需要在求的过程中维护一个pre数组表示这个点的前驱即可。很多最短路的变种都需要用这个算法。

最小生成树

Prim 算法

类比 Dijkstra 算法，我们维护一个集合 S，表示这个集合中 的生成树已经确定了。

算法流程和Dijkstra一样，唯一的区别是用w(u, v) 去更新 dv 而不是用 du + w(u, v)。

时间复杂度 O(n ² )，同样可以用堆优化。

Kruskal 算法

前置知识

并查集算法

并查集主要用于解决一些元素分组的问题。它管理一系列不相交的集合，并支持两种操作：

合并：把两个不相交的集合合并为一个集合。

查询：查询两个元素是否在同一个集合中。

优化

路径压缩（O(logn)）+安值合并（O(logn)）→O(αn)（αn在10⁸数据内不超过4，可视为常数）

代码

find(int x)
{
    return x==pa[x]?x:pa[x]=find(pa[x])
}

因为是求的最小生成树，所以我们用贪心的思路，把所有的边权从小到大排序，然后一条一条尝试加入，用并查集维护连通性。

可以发现这样一定能得到原图的最小生成树。

证明

如果某一条边 (u, v) 不属于最小生成树，那么考虑最小生成树上 连接 u, v 的路径，这上面一定有一条边权不小于 w(u, v) 的边 （因为我们是从小到大枚举的所有边），这样替换后答案一定不会变劣。

时间复杂度 O(m log m)。

Kruskal 重构树

前置知识

dfs（深度优先搜索）

LCA（最近公共祖先）

在一棵没有环的树上，每个节点肯定有其父亲节点和祖先节点，而最近公共祖先，就是两个节点在这棵树上深度最大的公共的祖先节点。

LCA主要是用来处理当两个点仅有唯一一条确定的最短路径时的路径。

树上倍增

用于求LCA（最近公共祖先）。

倍增的思想是二进制。

首先开一个n×logn的数组，比如fa[n][logn],其中fa[i][j]表示i节点的第2^j个父亲是谁。

然后，我们会发现一个性质：

fa[i][j]=fa[fa[i][j-1]][j-1]

用文字叙述为：i的第2^j个父亲 是i的第2^(j-1)个父亲的第2^(j-1)个父亲。

这样，本来我们求i的第k个父亲的复杂度是O(k)，现在复杂度变成了O(logk)。

 

Kruskal 重构树是基于 Kruskal 最小生成树算法的一种算 法，它主要通过将边权转化为点权来实现。

流程

将所有边按照边权排序，设 r(x) 表示 x 所在连通块的根节点。（注意这里要用并查集）

枚举所有的边 (u, v)，若 u, v 不连通，则新建一个点 x，令 x 的权值为 w(u, v)。 连接 (x, r(u)) 和 (x, r(v))。 令 r(u) = r(v) = x。

不断重复以上过程，直到所有点均连通。

 

时间复杂度 O(m log m)。

性质

这样，我们就得到了一棵有 2n − 1 个节点的二叉树，其中叶节点为原图中的点，其余的点代表原图中的边，并且满足父节点权值大于等于子节点。

它有什么用呢？

求 u, v 之间路径上的最大边权 → 求重构树上 u, v 两个点的 LCA。

只保留边权小于等于 x 的边形成的树 → 重构树上点权小于 等于 x 的点的子树。

 

Borůvka 算法

前置知识

距离

（x₁,y₁）（x₂,y₂）

曼哈顿距离：|x₁-x₂|+|y₁-y₂|

切比雪夫距离：max(|x₁-x₂|,|y₁-y₂|

欧几里得距离：√[(x₁-x₂)²+(y₁-y₂)²]

曼哈顿距离与切比雪夫距离的相互转化

两者之间的关系

我们考虑最简单的情况，在一个二维坐标系中，设原点为(0,0)。

如果用曼哈顿距离表示，则与原点距离为1的点会构成一个边长为2–√2的正方形。

 

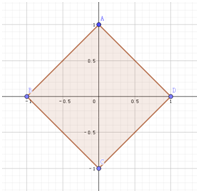
如果用切比雪夫距离表示，则与原点距离为1的点会构成一个边长为2的正方形。

 

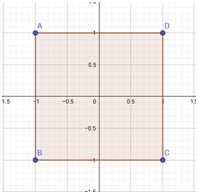
对比这两个图形，我们会发现这两个图形长得差不多，他们应该可以通过某种变换互相转化。

事实上,

将一个点(x,y)的坐标变为(x+y,x−y)后,原坐标系中的曼哈顿距离 =新坐标系中的切比雪夫距离。

将一个点(x,y)的坐标变为(（x+y）/2,（x−y）/2) 后,原坐标系中的切比雪夫距离 = 新坐标系中的曼哈顿距离。

（注意：切比雪夫距离转曼哈顿距离要再除以二）

 用处

切比雪夫距离在计算的时候需要取max，往往不是很好优化，对于一个点，计算其他点到该的距离的复杂度为O(n)。

而曼哈顿距离只有求和以及取绝对值两种运算，我们把坐标排序后可以去掉绝对值的影响，进而用前缀和优化，可以把复杂度降为O(1)。

 

第三种求最小生成树的算法，虽然比较冷门但是很多题需要用到这个算法。

我们维护当前形成的所有连通块，接下来对于每一个连通块，找到边权最小的出边，然后合并两个连通块。

不断重复这个操作，直到整张图变成一个连通块。

由于每次操作连通块数量至少减半，所以时间复杂度最坏为 O((n + m) log n)，随机图的话复杂度可以降到 O(n + m)。

Tarjan算法

Tarjan 算法不是某个特定的算法，而是一群算法。

强连通分量

割点/割边/桥

点双连通分量

边双连通分量

离线 O(n) 求 LCA

此外还有很多 Tarjan 独立/合作创造的算法：

Splay，LCT， 斐波那契堆，斜堆，配对堆，可持久化数据结构，……

有向图——强连通分量

如果对于两个点 u, v，同时存在从 u 到 v 的一条路径和从 v 到 u 的一条路径，那么就称这两个点强连通。

如果一张图的任意两个点均强连通，那么就称这张图为强连通图。

强连通分量指的是一张有向图的极大强连通子图。 （极大≠最大）

Tarjan 算法可以用来找出一张有向图的所有强连通分量。

我们用 dfs的方式来找出一张图的强连通分量。

建出 dfs 树，记录一下每一个节点的时间戳(dfn)，然后我们考虑强连通分量应该满足什么条件。

我们可以再记录一个 low 数组，表示每一个点能够到达的最小的时间戳，如果一个点的 dfn=low，那么这个点下方就形成了一个强连通分量。

在 dfs 的过程中，对于 (u, v) 这条边：

若 v 未被访问，则递归进去 dfs 并且用 low[v] 更新 low[u]。

若 v 已经被访问并且在栈中，则直接用 dfn[v] 更新 low[u]。

最后如果 dfn[u]=low[u]，则直接把栈中一直到 u 的所有点 拿出来作为一个强连通分量。

时间复杂度 O(n)。

有向图——缩点

跑出来强连通分量之后，我们可以把一个强连通分量看成一 个点。

接下来枚举所有的边，如果是一个强连通分量里的就忽略， 否则连接两个对应的强连通分量。这个操作称为缩点。

缩点后就变成了一张有向无环图，处理连通性问题的时候会方便很多。

无向图——割点

对于一张无向图，我们希望求出它的割点。

无向图的割点定义为删掉这个点之后，连通块数量会发生改变的点。

类比上面，我们还是记录一下 dfn（时间戳）和 low。

对于 u 的一个子节点 v，若 dfn[u]≤low[v]，则 u 是割点（因 为 v 无法绕过 u 往上走）。

不过需要注意两点：

根节点不能用这种方法，而是应该看它的子节点数量是否大于等于 2，如果是那么根节点就是割点。

枚举出边的时候要特判掉父子边的情况。

无向图——桥

无向图的桥定义为删掉这条边后，连通块数量会发生改变的边。

和上面的方法几乎一模一样，唯一的区别是判断dfn[u]<low[v]而不是dfn[u]≤low[v]。（如果从 v 出发连 u 都无法 到达，那么 (u, v) 就是一个桥边）

甚至连根节点都不需要特判了。

无向图——点/边双连通分量

如果两个点之间存在两条点互不相交的路径，那么就称这两个点是点双连通的。

如果两个点之间存在两条边互不相交的路径，那么就称这两个点是边双连通的。

其余的定义参考强连通分量。                       

割点将整张图分成了若干个点双连通分量，并且一个割点可以在多个点双连通分量中。

而桥则把整张图拆成了若干个边双连通分量，并且桥不在任意一个边双连通分量中。

魔改一下强连通分量算法即可。

当然，无向图也可以缩点，不过主要还是可以用来建圆方树。

二分图匹配

前置知识

匹配

在图论中，一个匹配是一个边的集合， 其中任意两条边都没有公共顶点。

最大匹配

一个图所有匹配中，所含匹配边数最多的匹配， 称为这个图的最大匹配。

如果要求一般图的最大匹配，需要用 O(n ³ ) 的带花树，至少 是 NOI+ 的算法。在联赛阶段，我们一般只关注二分图的匹配问题。

最大匹配——匈牙利算法

完美匹配

如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。

二分图

如果一个图的顶点能够被分为两个集合 X, Y，满 足每一个集合内部都没有边相连，那么这张图被称作是一张二分图。

（dfs可以判断一张图是否是二分图）

交替路

从一个未匹配点出发，依次经过非匹配边——匹配 边——非匹配边——……形成的路径叫交替路。

增广路

从一个未匹配点出发，依次经过非匹配边——匹配 边——非匹配边——……——非匹配边，最后到达一个未匹配点形成的路径叫增广路。

注意到，一旦我们找出了一条增广路，将这条路径上所有匹配边和非匹配边取反，就可以让匹配数量+1。

匈牙利算法就是基于这个原理。

假设我们已经得到了一个匹配，希望找到一个更大的匹配。

我们从一个未匹配点出发进行 dfs（深度优先搜索），如果找出了一个增广路， 就代表增广成功，我们找到了一个更大的匹配。

如果增广失败，可以证明此时就是最大匹配。

由于每个点只会被增广一次，所以时间复杂度是 O(n(n + m))。

二分图最大权匹配——KM 算法

现在我们把所有的边都带上权值，希望求出所有最大匹配中权值之和最大的匹配。

我们的思路是给每一个点赋一个“期望值”，也叫作顶标函数 c，对于 (u, v) 这条边来说，只有 c(u) + c(v) = w(u, v) 的时 候，才能被使用。

容易发现，此时的答案就是 ∑c(i)。

初始，我们令左边所有点的 c(u) = maxv w(u, v)，也就是说最理想的情况下，每一个点都被权值最大的出边匹配。

接下来开始增广，每次只找符合要求的边。我们定义只走这些边访问到的子图为相等子图。

如果能够找到增广路就直接增广，否则，就把这次增广访问到的左边的所有点的 c − 1，右边所有点的 c + 1。

经过这样一通操作，我们发现原来的匹配每一条边仍然满足条件。同时由于访问到的点左边比右边多一个（其余的都匹配上了），所以这样会导致总的权值−1。

接下来再尝试进行增广，重复上述过程。直接这样做时间复 杂度是 O(n ³ c) 的。（进行 n 次增广，每次修改 c 次顶标，访问所有 n ² 条边）

优化

由于修改顶标的目标是让相等子图变大，因此可以每次加减 一个最小差值 delta。这样每次增广只会被修改最多 n 次顶标，时间复杂度降到 O(n ⁴ )。

注意到每次重新进行 dfs（深度优先搜索） 太不优秀了，可以直接进行 bfs， 每次修改完顶标之后接着上一次做。时间复杂度降到 O(n ³ )。

技巧

最小点覆盖

选取最少的点，使得每一条边的两端至少有一 个点被选中。

二分图的最小点覆盖 = 最大匹配

证明

1.由于最大匹配中的边必须被覆盖，因此匹配中的每一个点对 中都至少有一个被选中。

2.选中这些点后，如果还有边没有被覆盖，则找到一条增广路，矛盾。

最大独立集：选取最多的点，使得任意两个点不相邻。

最大独立集 = 点数-最小点覆盖

证明

1.由于最小点覆盖覆盖了所有边，因此选取剩余的点一定是一个合法的独立集。

2.若存在更大的独立集，则取补集后得到了一个更小的点覆盖，矛盾。

最小边覆盖：选取最少的边，使得每一个点都被覆盖。

最小边覆盖 = 点数-最大匹配

证明

1.先选取所有的匹配边，然后对剩下的每一个点都选择一条和 它相连的边，可以得到一个边覆盖。

2.若存在更小的边覆盖，则因为连通块数量 = 点数-边数，这 个边覆盖在原图上形成了更多的连通块，每一个连通块内选一条边，我们就得到了一个更大的匹配。

最小不相交路径覆盖：一张有向图，用最少的链覆盖所有的点，链之间不能有公共点。

将点和边分别作为二分图的两边，然后跑匹配，最小链覆盖 = 原图点数-最大匹配。

最小可相交路径覆盖：一张有向图，用最少的链覆盖所有的 点，链之间可以有公共点。

先跑一遍传递闭包，然后变成最小不相交路径覆盖。

补充

小黄鸭调试法

当你的代码出现问题的时候，

将小黄鸭想象成你的同学，

将你的代码一行一行地讲给它，

也许讲到一半你就知道问题出在哪了。

不要定义以下变量名

next,abs,x1,y1,size……

并非原创，仅是整理，请见谅