noip基础算法（未完成）

枚举

对于一些简单的题目，我们或许不需要用什么太巧妙的方法，只需要把所有的可能性列举出来，然后逐一试验就可以了。

方法

通过事先把各种可能发生的事情都列举一遍，为后面求解提供结果。

常见类型

枚举排列

枚举子集

递归

基本思想

通过不断调用自己，把一个复杂问题层层转化为规模更小的相似问题。

补充

next permutation/prev permutation(全排列算法)

STL提供了两个用来计算排列组合关系的算法，分别是next permutation（“下一个”排列组合）和prev permutation（“前一个”排列组合）。首先我们需要了解什么是“下一个”排列组合，什么是“前一个”排列组合。

考虑三个字符所组成的序列{a,b,c}，这个序列有六个可能的排列组合：abc，acb，bac，bca，cab，cba。这些排列组合根据less-than操作符做字典顺序(lexicographical)的排序。也就是说，abc是第一个排列组合，因为每一个元素都小于其后的元素。acb是次一个排列组合，因为它是固定了a(序列内最小元素)之后所做的新组合。

同样道理，那些固定b(序列中次小元素)而做的排列组合，在次序上将先于那些固定c而做的排列组合。以bac和bca为例，bac在bca之前，因为次序ac小于序列ca。面对bca，我们可以说其前一个排列组合是bac，而其后一个排列组合是cab。序列abc没有“前一个”排列组合，cba没有“后一个”排列组合。

next permutation()会取得[first,last)所标示的序列的下一个排列组合，如果没有下一个排列组合，便返回false；否则返回true。这个算法有两个版本。版本一使用元素型别所提供的less-than操作符来决定下一个排列组合，版本二则是以仿函数comp来决定。

算法思想
首先从最尾端开始往前寻找两个相邻元素，令第一元素为i,第二元素为ii,且满足i<ii。

找到这样一组相邻元素后，再从最尾端开始往前检验，找出第一个大于i的元素，令其为j，将i,j元素对调(swap)。

再将ii之后的所有元素颠倒(reverse)排序。

举个例子，假设有序列{0,1,2,3,4}，下图便是套用上述演算法则，一步一步获得“下一个”排列组合。图中只框出那符合“一元素为i,第二元素为ii,且满足i<ii ”的相邻两元素，至于寻找适当的j、对调、逆转等操作未显示出。

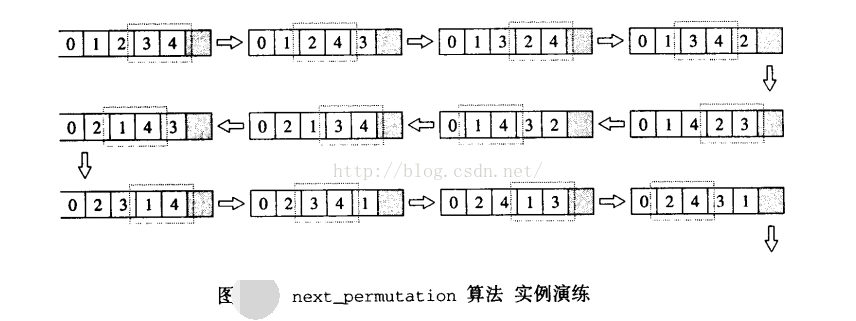
以下是版本一的实现。版本二类似，就不列出来了。

template<calss BidrectionalIterator>
bool next_permutation(BidrectionalIterator first,BidrectionalIterator last)
{
    if(first == lase) return false; /* 空区间 */
    BidrectionalIterator i = first;
    ++i;
    if(i == last) return false;  /* 只有一个元素 */
    i = last;                    /* i指向尾端 */  
    --i;
    for(;;)
    {
        BidrectionalIterator ii = i;
        --i;
        /* 以上锁定一组(两个)相邻元素 */
        if(*i < *ii)           /* 如果前一个元素小于后一个元素 */
        {
            BidrectionalIterator j = last; /* 令j指向尾端 */
            while(!(*i < *--j));     /* 由尾端往前找，直到遇到比*i大的元素 */
            iter_swap(i,j);          /* 交换i,j */
            reverse(ii,last);        /* 将ii之后的元素全部逆序重排 */
            return true;
        }
        if(i == first)       /* 进行至最前面了 */
        {
            reverse(first,last);    /* 全部逆序重排 */
            return false;
        }
    }
}

应用

输出序列{1,2,3,4}字典序的全排列。

#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
    int ans[4]={1,2,3,4};
    sort(ans,ans+4);    /* 这个sort可以不用，因为{1，2，3，4}已经排好序*/
    do                             /*注意这步，如果是while循环，则需要提前输出*/
    {
        for(int i=0;i<4;++i)
            cout<<ans[i]<<" ";
        cout<<endl;
    }while(next_permutation(ans,ans+4));
    return 0;
}

算出集合{1, 2, …, m}的第n个排列

样例：

7个数的集合为{1, 2, 3, 4, 5, 6, 7}，要求出第n=1654个排列。

(1654 / 6!)取整得2，确定第1位为3（从0开始计数），剩下的6个数{1, 2, 4, 5, 6, 7}，求第1654 % 6!=214个序列；

(214 / 5!)取整得1，确定第2位为2，剩下5个数{1, 4, 5, 6, 7}，求第214 % 5!=94个序列；

(94 / 4!)取整得3，确定第3位为6，剩下4个数{1, 4, 5, 7}，求第94 % 4!=22个序列；

(22 / 3!)取整得3，确定第4位为7，剩下3个数{1, 4, 5}，求第22 % 3!=4个序列；

(4 / 2!)得2，确定第5为5，剩下2个数{1, 4}；由于4 % 2!=0，故第6位和第7位为增序<1 4>；

因此所有排列为：3267514。

#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
    int ans[7]={1,2,3,4,5,6,7};
    sort(ans,ans+7);  /* 同上可以不用sort */
    int n=0; 
    do                             //注意这步，如果是while循环，则需要提前输出
    {
        if(n == 1654)
        {
             for(int i=0;i<7;++i)
            cout<<ans[i];
            cout<<endl;
            break;
        }
        n++;
     }while(next_permutation(ans,ans+7));
    return 0;
}

给定一个排列，算出这是第几个排列

和上一个问题的推导过程相反。

如3267514：

后6位的全排列为6！，3为{1, 2, 3 ,4 , 5, 6, 7}中第2个元素（从0开始计数），故2*720=1440；

后5位的全排列为5！，2为{1, 2, 4, 5, 6, 7}中第1个元素，故1*5!=120；

后4位的全排列为4！，6为{1, 4, 5, 6, 7}中第3个元素，故3*4!=72；

后3位的全排列为3！，7为{1, 4, 5, 7}中第3个元素，故3*3!=18；

后2位的全排列为2！，5为{1, 4, 5}中第2个元素，故2*2!=4；

最后2位为增序，因此计数0，求和得：1440+120+72+18+4=1654

这个的代码实现，可以用一个数组a保存3267514,然后while调用next_permutation(),用n计数，每次与数组a比较，相等则输出n;