ST表

定义

·也叫RMQ算法
·给定序列，要求O(1)求区间（l，r）的最小值

·F[i][j]代表i到i+2^j-1的最小值。
·F[i][j]=min(f[i][j-1],f[i+2^(j-1)][j-1])
·O(nlogn)预处理

设k为最大的正整数满足2^k<=r-l+1 Min(l,r)=min(f[l][k],f[r-2^k+1][k]) 如图：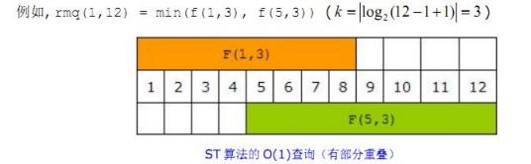

板子题

洛谷P3865 ST表

题目背景

这是一道 ST 表经典题——静态区间最大值

请注意最大数据时限只有 0.8s，数据强度不低，请务必保证你的每次查询复杂度为 O(1)O(1)O(1)。若使用更高时间复杂度算法不保证能通过。

如果您认为您的代码时间复杂度正确但是 TLE，可以尝试使用快速读入：

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<"0"||ch>"9"){if (ch=="-") f=-1;ch=getchar();}
	while (ch>="0"&&ch<="9"){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

函数返回值为读入的第一个整数。

快速读入作用仅为加快读入，并非强制使用。

题目描述

给定一个长度为 NNN 的数列，和 M M M 次询问，求出每一次询问的区间内数字的最大值。

输入格式

第一行包含两个整数 N,MN,MN,M，分别表示数列的长度和询问的个数。

第二行包含 NNN 个整数（记为 aia_iai​），依次表示数列的第 iii 项。

接下来 MMM 行，每行包含两个整数 li,ril_i,r_ili​,ri​，表示查询的区间为 [li,ri][l_i,r_i][li​,ri​]。

输出格式

输出包含 MMM 行，每行一个整数，依次表示每一次询问的结果。

Code(很蒟蒻）

#include <bits/stdc++.h>
using namespace std;
const int MAXN=1e6+10;
inline int read()//快速读入 
{
    char c=getchar();
	int x=0,f=1;
    while(c<"0"||c>"9"){
	if(c=="-")f=-1;
	c=getchar();
}
    while(c>="0"&&c<="9"){
		x=x*10+c-"0";c=getchar();
	}
    return x*f;
}
int Max[MAXN][21];
int st(int l,int r)//ST表 
{
    int k=log2(r-l+1); 
    return max(Max[l][k],Max[r-(1<<k)+1][k]);
}
int main(){
    int N=read(),M=read();
    for(int i=1;i<=N;i++) 
		Max[i][0]=read();
    for(int j=1;j<=21;j++)
        for(int i=1;i+(1<<j)-1<=N;i++)
            Max[i][j]=max(Max[i][j-1],Max[i+(1<<(j-1))][j-1]);
    for(int i=1;i<=M;i++)
    {
        int l=read(),r=read();
        printf("%d
",st(l,r));
    }
    return 0;
}  

分析

题中时间限制只有800ms，时间复杂度尤为重要。
本蒟蒻最后两个点就超时了
尽量使用快速读入

人生忠告：

不要过于依赖cin cout 二者并不是万金油，一些卡时间的题容易超时
printf YYDS