FireMonkey3D之中国象棋程序（三）初步搜索算法

声明：本程序设计参考象棋巫师源码（开发工具dephi 11，建议用delphi 10.3以上版本）。

这一章计划初步实现搜索算法，前两章基本上按照我自己对中国象棋的理解来设计程序，从这章开始参照象棋巫师算法。

3.1、局面评价 　

中国象棋共有7种棋子：将（帅）、士、相、马、车、炮、兵，局面评价中最关键的因素是每种棋子的价值，子力价值是跟它的绝对位置相关的。比如兵(卒)，过河前基本上没有什么威胁，子力价值就很低，过河后分数大涨，越接近九宫分数就越高，九宫中心甚至接近一个马或炮的值。再比如马，在卧槽的位置和在挂角的位置对将（帅）的影响非常大，在此位置子力评分很高。如此一来，每个兵种就都会有一个与绝对位置相关的价值，因此我们定义一个三维常量数组：vlPc:array [0..6,0..9,0..8] of Byte（从“象眼”中照搬过来的），这个子力价值表水平左右对称，以红方为基准，黑方使用时只须颠倒纵向数据即可。

我们在TPieceMove内定义两个常量：vlRed, vlBlack:Integer;   用来记录红、黑双方的子力价值；定义Evaluate函数来评价局面分，即红黑双方的子力价值差，先走棋再加3分。我们可以每次走棋后，全盘搜索每个棋子的位置来计算局面分，但是这样做太浪费时间了，因为根本没有必要每次都把棋盘扫描一遍。我们定义了两个函数来实现每步走棋计算分值：调用 AddPiece (放一枚棋子)和 DelPiece (取走一枚棋子)，可以趁这个机会更新 Evaluate，这样的局面评价函数已经足够了。

3.2、极大极小搜索算法

以上均为准备工作。现在我们先从最简单的搜索算法学起：极大极小搜索算法。这个算法这样首先这样评价局面：

　 如果黑方被将死了，那么评价函数返回一个充分大的正数；如果红方被将死了，那么返回一个充分大的负数。如果红方是赢棋或者很有希望赢，那么函数通常会返回正数；如果黑方是赢棋或者很有希望赢，那么返回负数；如果棋局是均势或者是和棋，那么返回在零左右的数值。

     按照搜索算法的思路，我们先定义常量：MATE_VALUE = 10000; 最高分值，即将死的分值。极大搜索时，初始化始最优值为负无穷，即—MATE_VALUE；极小搜索时，为正MATE_VALUE，这样定义的好处是可以确定没有走过任何棋。

　　简要描述一下这个函数是如何运作的。假设根局面(棋盘上当前局面)是红方走，先生成红方所有合理走法，逐一走这些走法，调用“maxSearch”函数，生成黑方所有合理着法。在每个后续局面中，调用的是“MinSearch”函数，它对局面作出评价并返回。由于现在是红方走，因此红方需要让评价尽可能地大，能得到最大值的那个着法被认为是最好的，因此返回这个着法的评价。“minSearch”函数正好相反，当黑方走时调用“Min”函数，而黑方需要尽可能地小，因此选择能得到最小值的那个着法。这两个函数是互相递归的，即它们互相调用，直到达到所需要的深度为止。当函数到达最底层时，它们就返回“Evaluate”函数的值。如果在深度为1时调用“MinMax”函数，那么“Evaluate”函数在走完每个合理着法之后就调用，选择一个能达到最佳值的那个着法导致的局面。如果层数大于1，那么另一方有权选择局面，并找一个最好的。

　　举个例子，电脑为A，人类为B，A在走棋之前需要思考，A走了某一步后，看看B有哪些走法，B又不傻，所以B肯定是要选择让A得分最少的走法走棋，而A会选择在所有走法中B认为得分最少的走法中分值最高的走法，也就是说Ａ的走法取决于Ｂ，反之亦然。听起来大概会比较抽象比较绕吧，试着多读几遍，多理解理解。
通过极大极小搜索算法，电脑就可以初步自动回应走棋了。极大极小搜索算法可以合成负极大搜索，搜索过程如下图：

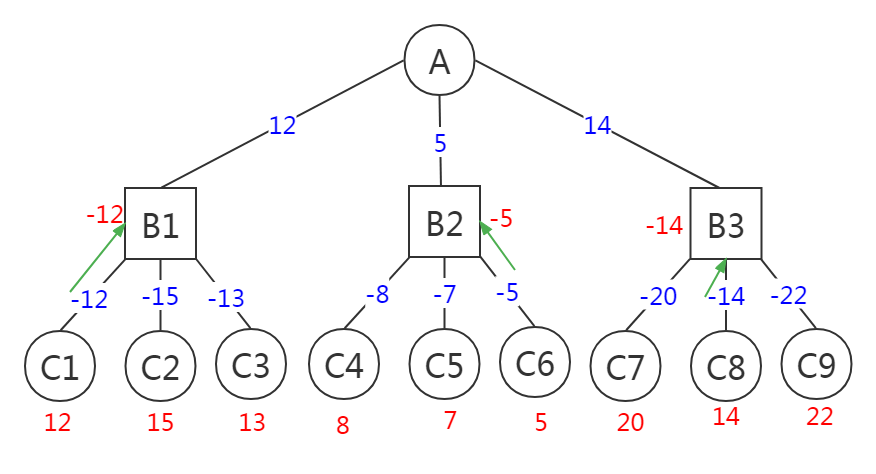
红色数字是当前节点的分值，蓝色数字是父节点对子节点返回值取负后的值。

搜索进行到C1、C2、C3时，要做评估，得到的估值是12、15、13。由于此时轮到红方走棋，表示红方在三个局面分别有12、15、13的优势。在极大极小搜索中，要在B1求这三个局面估值的最小值。现在我们可以这样来看，黑方在C1、C2、C3的优势分别为-12、-15、-13。黑方显然在B1点需要对三个局面做一个选择，选择的目标当然是优势最大化。可以这样表示：max(-12, -15, -13)；

在极大极小搜索中，B1是黑方走棋，是极小点，应该求最小值。现在由于多加了一个负号，也变成求极大值了，B1点也成了极大点。

黑方在B1、B2、B3分别取得了-12、-5、-14的优势，对于红方来讲，则在这三个点分别有12、5、14的优势。所以在A点，轮到红方走棋，它会在B1、B2、B3中选择最大值，即：max(12, 5, 14)，这里看出A的选择了吗？

代码如下：

function negaMaxSearch (depth:Integer):Integer;
var
  vlBest,i,value:Integer;
  mvs:TArray<TMoves>;
  s,d:TPoint;
  id:Byte;
begin
  // 深度为0，调用评估函数并返回分值
  if depth = 0 then
    Exit(pcMove.evaluate);
  vlBest:=-MATE_VALUE;		// 初始最优值为负无穷
  mvs:= pcmove.generateMoves;	// 生成当前局面的所有走法
  value:= 0;
  for i:= 0 to Length(mvs)-1 do
  begin
    s:=mvs[i].src;
    d:=mvs[i].dest;
    if not pcMove.makeMove(s,d,id) then Continue;
    value:=-negaMaxSearch(depth - 1);
    PcMove.undoMakeMove(s,d,id);
    if value > vlBest then
      vlBest:= value;
    if depth = MINMAXDEPTH then
      Search.mvResult:= mvs[i];
  end;
  Result:=vlBest;// 返回当前节点的最优值
end;