wen 编程最新 2024-01-31

数据结构与算法(二)

双向链表

单向链表的缺点

从前面的练习题，包括实现单向链表中会发现 单向链表 的以下问题：

查找方向 只能是单向
不能自我删除

需要靠辅助节点，要找到删除节点的上一个节点和删除节点，才能完成删除

而以上问题，双向链表：

可以双向查找
可以自我删除

双向链表的思路分析

双向链表的结构如上图所示，每个节点都有 pre 和 next 变量，所以它可以往前查找或则往后查找。

那么下面先分析下双向链表的：遍历、添加、删除操作思路，之后再去实现：

遍历：和单向链表类似，只是可以双向遍历了
修改：和单向链表一样的方式
添加：默认添加到双向链表的最后一个节点
1. temp.next = newNode
2. newNode.pre = temp
删除

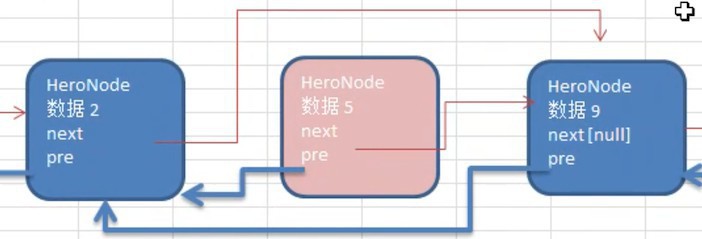
如上图所示，双向链表可以自我删除：

遍历找到要删除的那个节点 temp
temp.next.pre = temp.pre
temp.pre.next = temp.next

代码实现

//定义节点
class HeroNode2{
    public int no;//英雄编号
    public String name;//英雄名称
    public String nickName;//英雄花名
    public HeroNode2 next;//当前节点的下一个节点
    public HeroNode2 pre;//指向当前节点的前一个节点

    public HeroNode2(int no,String name,String nickName){
        this.no = no;
        this.name = name;
        this.nickName = nickName;
    }
    //方便遍历显示信息
    @Override
    public String toString() {
        return "HeroNode{" +
                "no=" + no +
                ", name="" + name + """ +
                ", nickName="" + nickName + """ +
                "}";
    }
}
//定义双向链表
class DoubleLinkedList{
    private HeroNode2 head;//定义头节点

    public DoubleLinkedList(){
        head = new HeroNode2(0,"","");//创建双向链表的头节点
    }

    //返回头节点
    public HeroNode2 getHead(){
        return head;
    }

    //双向链表的遍历
    public void list(){
        //借助辅助变量遍历
        HeroNode2 temp = head.next;
        while(true){
            if(temp == null){
                break;
            }
            System.out.println(temp);
            temp = temp.next;
        }
    }
    //双向链表的添加元素，添加在最后，无序添加
    public void add(HeroNode2 h){
        HeroNode2 temp = head;//获取头节点
        while(true){
            if(temp.next == null){
                break;//找到最后一个元素
            }
            temp = temp.next;
        }
        //添加双向链表节点
        temp.next = h;
        h.pre = temp;
    }
    //有序添加元素
    public void addOrder(HeroNode2 h){
        HeroNode2 temp = head;
        boolean flag = false;//是否存在重复添加元素
        while(true){
            if(temp.next == null){
                break;//已经遍历到结尾
            }
            if(temp.next.no > h.no){
                break;//找到要添加的位置
            }else if(temp.next.no == h.no){
                flag = true;
                break;//重复添加
            }
            temp = temp.next;
        }
        if(flag){
            //重复添加
            System.out.printf("添加失败，元素节点%d已经存在",h.no);
        }
        //添加元素
        h.pre = temp;
        h.next = temp.next;
        if(temp.next != null){//如果添加的元素不是最后一个
            temp.next.pre = h;
        }
        temp.next = h;
    }

    //修改节点信息
    public void update(HeroNode2 h){
        if(head.next == null){
            System.out.println("单链表为空，修改失败");
            return;
        }
        HeroNode2 temp = head.next;
        boolean flag = false;//用于记录是否找到要修改的元素
        while(true){
            if(temp == null){//已经遍历到最后
                break;
            }else if(temp.no == h.no){//找到要修改的元素
                flag = true;
                break;
            }
            temp = temp.next;
        }
        if(flag){//修改信息
            temp.name = h.name;
            temp.nickName = h.nickName;
        }else{
            System.out.printf("修改失败，没有找到%d节点元素",h.no);
        }
    }

    //删除指定节点
    public void remove(int no){
        if(head.next == null){
            System.out.println("链表为空，删除失败");
            return;
        }
        HeroNode2 temp = head.next;//从第一个元素开始查找
        boolean flag = false;//记录是否找到对应节点
        while(true){
            if(temp == null){//已经遍历到最后
                break;
            }else if(temp.no == no){//找到要删除的元素节点
                flag = true;
                break;
            }
            temp = temp.next;
        }
        if(flag){
            temp.pre.next = temp.next;
            if(temp.next != null){
                temp.next.pre = temp.pre;
            }
        }else{//没有找到要删除的节点
            System.out.printf("删除失败，没有找到要%d节点",no);
        }
    }
}

单向环形链表-Josephu 问题

应用场景-约瑟夫问题

约瑟夫（Josephu）问题，也就是丢手帕问题，他的规则如下

有编号为 1 ~ n 的 n 个人围坐在一起
约定编号为 K( 1 <= k <=n) 的人从 1 开始报数
数到 m 的那个人出列，它的下一位又从 1 开始报数

循环以上过程，直到所有人都出列，并列出出列人的编号。

该问题其实可以使用 单循环链表（单向环形链表）来解决，思路如下：

先构成一个有 n 个节点的单循环链表
然后由 k 节点起从 1 开始计数
计数到 m 时，对应节点从链表中删除，然后从下一个节点又从 1 开始计数

循环以上过程，直到最后一个节点从链表中删除，算法结束

单向环形链表介绍

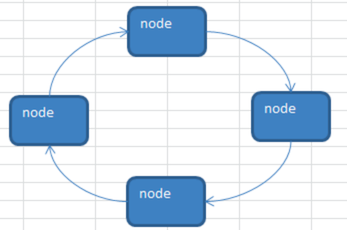
约瑟夫问题示意图

需求如下：

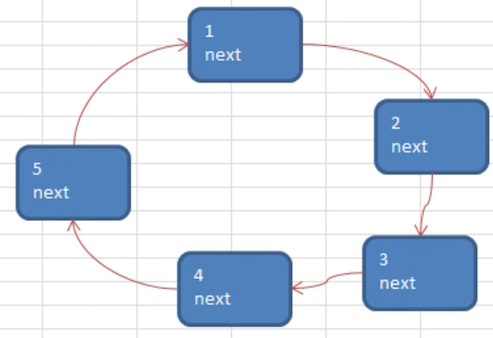
n=5：有 5 个人
k=1：从第一个人开始数
m=2：数两次

第一轮：2 出队列，1.next = 3

还剩下：1、3、4、5
第二轮：4 出队列，3.next = 5；（从 3 开始报数，第 2 个的出队列，也就是 4）

还剩下：1、3、5
第三轮：1 出队列，5.next = 3

还剩下：3、5
第四轮：5 出队列，3.next = 3

还剩下：3，自己的 next 就是自己
第五轮：3 出队列，队列中无元素，结束

那么最终的出队列顺序就是：2、4、1、5、3

约舍夫问题可以使用数组来解决，这里使用单向环形链表，比较好理解

创建环形链表的思路图解

环形链表添加思路

第 1 个节点被添加进来时

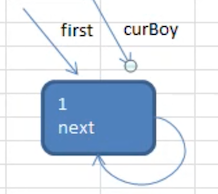
使用一个 first 变量来表示这是第一个节点，和带头节点的链表类似，第一个节点不能去改变他，使用 curBody 变量来辅助我们解决添加的过程，并让 first 指向自己，形成一个环形

第 2 个节点被添加进来时

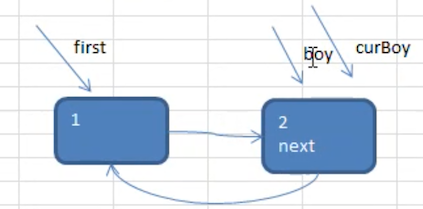
将该节点加入到已有的环形变量表

第 3 个节点被添加进来时

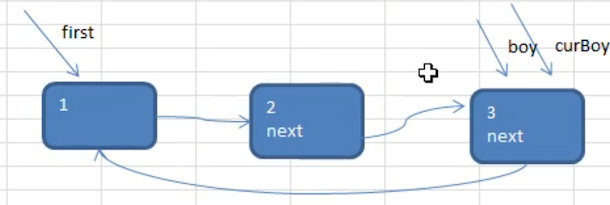
遍历环形链表

先让一个辅助变量 cur，指向 first 节点
通过一个 while 循环遍历该，当 cur.next = first 时，就遍历完了

环形链表实现代码

//定义节点
class Boy{
    private int no;//当前节点编号
    private Boy next;//当前节点的下一个节点

    public Boy(int no){
        this.no = no;
    }

    public int getNo() {
        return no;
    }

    public void setNo(int no) {
        this.no = no;
    }

    public Boy getNext() {
        return next;
    }

    public void setNext(Boy next) {
        this.next = next;
    }

    @Override
    public String toString() {
        return "Boy{" +
                "no=" + no +
                "}";
    }
}
//定义环形单链表
class CircleSingleLinkedList{
    private Boy first;
    //添加指定个数的节点
    public void addBoy(int nums){
      if(nums < 1){
          System.out.println("节点个数必须大于1");
          return;
      }
      Boy curBoy = null;
      for(int i = 1; i <= nums; i++){
          Boy h = new Boy(i);
          if(i == 1){
              //添加元素为第一个元素
              first = h;//first指向第一个元素
              h.setNext(first);//将当前节点的下一个节点设置为头节点
              curBoy = h;//将辅助变量指向头节点
          }else{
              //添加元素不是第一个元素
              curBoy.setNext(h);
              h.setNext(first);//将当前节点的下一个节点指向头部
              curBoy = curBoy.getNext();//将辅助变量指针后移
          }
      }
    }
    //遍历节点
    public void showBoy(){
      if(first == null){
          System.out.println("当前环形单链表为空");
          return;
      }
      //定义辅助变量，帮助遍历
      Boy curBoy = first;
      while(true){
          System.out.println(curBoy);
          if(curBoy.getNext() == first){
              break;//遍历结束
          }
          //指针后移
          curBoy = curBoy.getNext();
      }
    }
}

出圈思路分析

还是以这个需求来分析：

用户输入如下：

n=5：有 5 个人
k=1：从第一个人开始数
m=2：数两次

初始化时，需要一个 helper 辅助节点来表示first的前一个节点，如下图所示
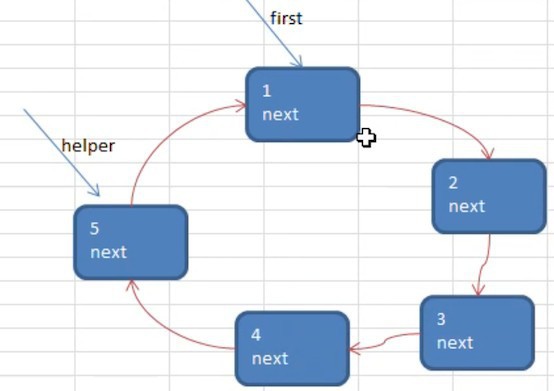
将 first 和 helper 定位到 k （从第几个小孩开始报数）将 first 和 helper 移动 k-1 次
小孩报数时：移动 first 到出圈的节点上，hepler 始终在 first 后面

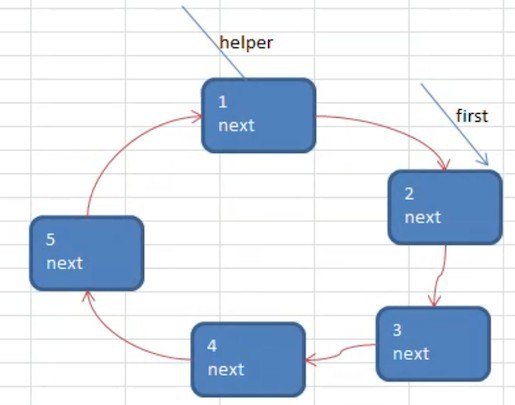
让 first 和 helper 同时移动 m-1 次，是因为 开始数数的人 也要占用一个位置：比如上图，从 first 开始，在编号 2 时，就数了 2 下了，它该出圈

小孩出圈

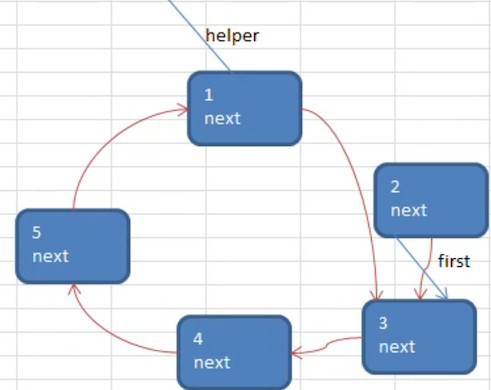
先将 first = first.next，然后将 helper.next = first，那么就如上图所示了，出圈的 first 被孤立出圈了，别人没有引用它了

注意：只有 小孩报数和出圈是重复 的，其他的只是这个游戏开始前的一些设置。

出圈代码实现

 //出圈实现

/**
     *
     * @param startNo 第几个开始数
     * @param countNum 每次数几个
     * @param nums 单向环形链表的总节点数
     */
public void countBoy(int startNo,int countNum,int nums){
    if(first == null || countNum < 1 || countNum > nums){
        System.out.println("参数不正确或者环形单链表为空");
        return;
    }
    //将helper移动到first前一个节点
    Boy helper = first;
    while(true){
        if(helper.getNext() == first){
            break;
        }
        helper = helper.getNext();//指针后移
    }
    //将first,helper移动到startNo处，需要将first，helper一起移动startNo-1次
    for(int j = 0; j < startNo-1; j++){
        first = first.getNext();
        helper = helper.getNext();
    }
    //找出圈元素
    while(true){
        if(helper == first){
            break;
        }
        for(int i = 0; i < countNum -1; i++){
            //移动指定次数
            first = first.getNext();
            helper = helper.getNext();
        }
        //出圈元素
        System.out.printf("小孩%d出圈
",first.getNo());
        //删除元素,first指针后移，删除指定元素
        first = first.getNext();
        helper.setNext(first);
    }
    System.out.printf("最后留在圈中小孩编号:%d
",first.getNo());
}

栈

栈快速入门

计算器需求

如上图：输入一个表达式 7*2*2-5+1-5+3-3，然后计算出他的结果。

问：计算机底层是如何运算得到结果的？对于计算机而言他接受到的是一个 字符串，怎么计算出来的？

针对这个问题，我们讨论的就是栈

栈介绍

stack 栈，是一个 先入后出（FILO，First In Last Out）的 有序列表。

是限制 线性表 中元素的插入和删除只能在线性表的 **同一端 **进行的一种特殊线性表：

栈顶（Top）：允许插入和删除的一端，为 变化的一端。称为栈顶
栈底（Bottom）：另一端为 固定的一端，称为栈底

根据上述定义，可知：

最先放入栈中元素在栈底
**最后 **放入栈中元素在栈顶

而删除元素则刚好相反：

最先放入栈中元素，最后删除
最后放入栈中元素，最先删除

可以参考下图的，入栈和出栈图示：

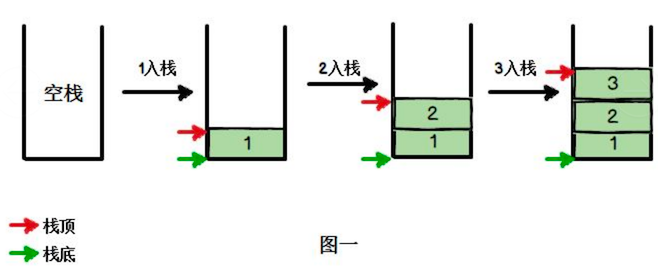
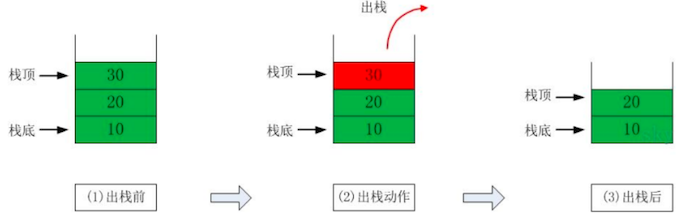
栈的应用场景

子程序的调用

在跳往子程序前，会先将 下个指令的地址 存到堆栈中，直到子程序执行完后再 将地址取出，以 回到原来的程序中。

如方法中调用方法。
处理递归调用

和子程序调用类似，只是除了存储下一个指令的地址外，也将参数、区域变量等数据存入堆栈中。
表达式的转换（中缀表达式转后缀表达式）与求值（实际解决）
二叉树的遍历
图形的深度优先（depth-first）搜索法

数组模拟栈

//使用数组模拟栈
class ArrayStack{
    private int maxTop;//表示栈的最大容量
    private int[] stack;//存储栈中数据
    private int top = -1;//指向栈顶元素，默认值-1

    public ArrayStack(int maxTop){
        this.maxTop = maxTop;
        stack = new int[maxTop];//创建栈数组
    }

    //判断栈是否满
    public boolean isFull(){
        return top == maxTop - 1;
    }

    //判断栈空
    public boolean isEmpty(){
        return top == -1;
    }

    //入栈
    public void push(int num){
        //先判断栈是否满了
        if(isFull()){
            System.out.println("入栈失败，栈满");
            return;
        }
        stack[++top] = num;
    }
    //出栈
    public int pop(){
        if(isEmpty()){
            throw new RuntimeException("栈中没有数据");
        }
        return stack[top--];
    }

    //显示栈中所有数据
    public void list(){
        if(isEmpty()){
            System.out.println("栈中没有数据");
            return;
        }
        for(int i = top; i >= 0; i--){
            System.out.printf("stack[%d] = %d
",i,stack[i]);
        }
    }
}

//测试代码
//测试栈
ArrayStack stack = new ArrayStack(4);
Scanner scanner = new Scanner(System.in);
String order = "";
boolean flag = true;
while(flag){
    System.out.println("show 显示所有数据");
    System.out.println("push 入栈");
    System.out.println("pop 出栈");
    System.out.println("exit 退出程序");
    System.out.println("请输入一个指令:");
    order = scanner.next();
    switch (order){
        case "show":
            stack.list();
            break;
        case "push":
            System.out.println("请输入一个数据:");
            int num = scanner.nextInt();
            stack.push(num);
            break;
        case "pop":
            try {
                int result = stack.pop();
                System.out.println(result);
            } catch (Exception e) {
                System.out.println(e.getMessage());
            }
            break;
        case "exit":
            flag = false;
            scanner.close();
            break;
        default:
            break;
    }
}
System.out.println("程序退出");

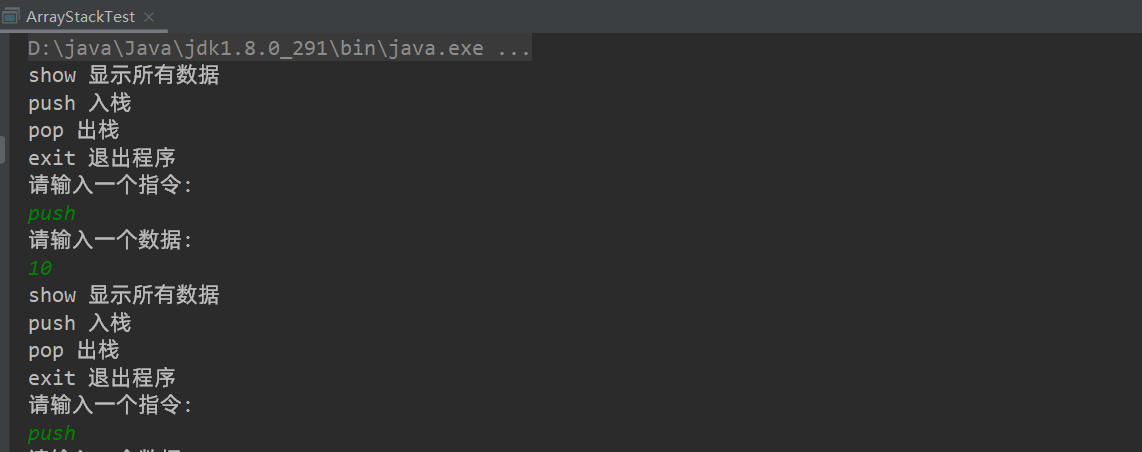
链表模拟栈

//定义链表节点
class Node{
    int data;//存储数据
    Node next;//指向下一个链表

    public Node(int data){
        this.data = data;
    }

    @Override
    public String toString() {
        return "Node{" +
                "data=" + data +
                "}";
    }
}
//使用链表定义栈
class LinkedListStack{
    private Node top;//定义一个栈顶指针，指向链表的第一个元素，也就是栈顶元素
    private int maxTop;//栈的最大长度
    private int size = 0;//记录栈中元素的个数

    public LinkedListStack(int maxTop){
        this.maxTop = maxTop;
    }

    //判断是否为空
    public boolean isEmpty(){
        return size == 0;
    }
    //判断是否为满
    public boolean isFull(){
        return size == maxTop;
    }
    //入栈
    public void push(int num){
        //判断栈是否满
        if(isFull()){
            System.out.println("栈满，添加失败");
            return;
        }
        Node h = new Node(num);
        h.next = top;
        top = h;
        size++;//元素个数增加
    }

    //出栈
    public int pop(){
        if(isEmpty()){
            throw new RuntimeException("出栈失败，栈为空");
        }
        Node temp = top;
        top = top.next;//指针后移
        size--;//元素个数减少
        return temp.data;
    }
    //遍历栈中元素
    public void list(){
        if(isEmpty()){
            System.out.println("栈中没有数据");
            return;
        }
        Node temp = top;
        for(int i = size - 1; i >= 0; i--){
            System.out.printf("stack[%d] = %d
",i,temp.data);
            temp = temp.next;//指针后移
        }
    }
    //获取栈中元素个数
    public int size(){
        return size;
    }
}

//测试代码
LinkedListStack stack = new LinkedListStack(4);
Scanner scanner = new Scanner(System.in);
String order = "";
boolean flag = true;
while(flag){
    System.out.println("show 显示所有数据");
    System.out.println("push 入栈");
    System.out.println("pop 出栈");
    System.out.println("size 获取栈长度");
    System.out.println("exit 退出程序");
    System.out.println("请输入一个指令:");
    order = scanner.next();
    switch (order){
        case "show":
            stack.list();
            break;
        case "push":
            System.out.println("请输入一个数据:");
            int num = scanner.nextInt();
            stack.push(num);
            break;
        case "pop":
            try {
                int result = stack.pop();
                System.out.println(result);
            } catch (Exception e) {
                System.out.println(e.getMessage());
            }
            break;
        case "size":
            System.out.println(stack.size());
            break;
        case "exit":
            flag = false;
            scanner.close();
            break;
        default:
            break;
    }
}
System.out.println("程序退出");

综合计算器

使用栈来实现综合计算器，比如，输入一个表达式：7*2*2-5+1-5+3-3 ，计算出这个表达式的结果

什么是中缀表达式

中缀表达式是一个通用的算术或 逻辑公式表示方法。 操作符 是以 中缀形式 处于操作数的中间（例：3 + 4），中缀表达式是人们常用的算术表示方法。

思路分析

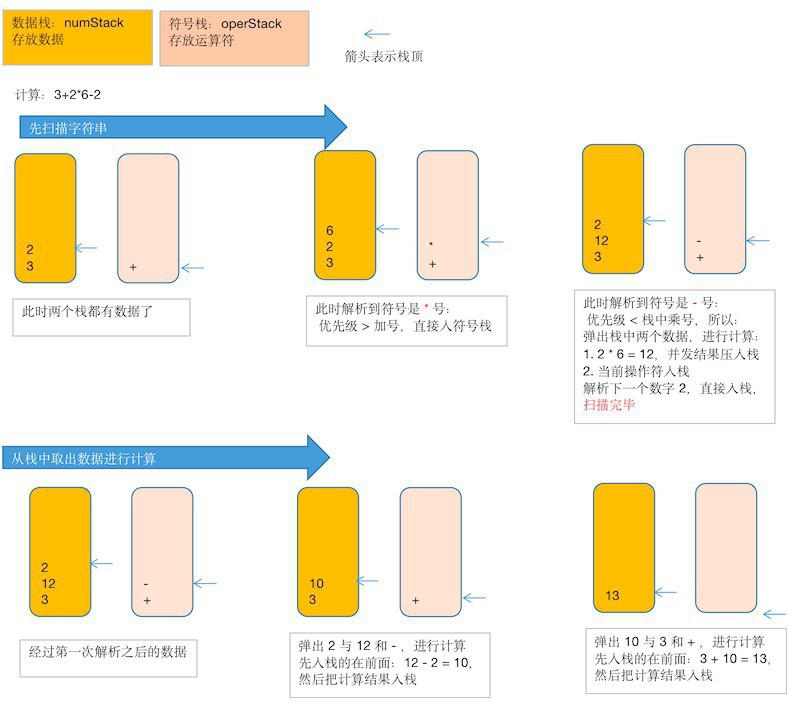
如上图：

需要先扫描字符串，可以通过一个 index 变量来辅助扫描
如果 发现是一个数字，直接入数栈
如果 发现是一个操作符，分以下情况：
- 当符号栈为空的时候，将符号直接添加到栈中
- 当符号栈不为空的时候，比较当前符号与符号栈顶元素的优先级进行比较，如果大于符号栈元素优先级则直接添加到符号栈中，小于等于符号栈中元素时，则从符号栈中弹出一个符号，从数栈中弹出两个数，进行计算，将结果加入数栈，再将当前符号添加到符号栈
当扫描完毕时：
1. 顺序的从数栈中弹出 2 个数，
2. 从符号栈中弹出 1 个操作符
3. 将他们进行计算，然后把计算结果压入数栈中
然后重复上面的三个步骤
最后在数栈中只会存在一个数值，它就是结果。

代码实现

//使用数组模拟栈
class ArrayStack2{
    private int maxTop;//表示栈的最大容量
    private int[] stack;//存储栈中数据
    private int top = -1;//指向栈顶元素，默认值-1

    public ArrayStack2(int maxTop){
        this.maxTop = maxTop;
        stack = new int[maxTop];//创建栈数组
    }

    //判断栈是否满
    public boolean isFull(){
        return top == maxTop - 1;
    }

    //判断栈空
    public boolean isEmpty(){
        return top == -1;
    }

    //入栈
    public void push(int num){
        //先判断栈是否满了
        if(isFull()){
            System.out.println("入栈失败，栈满");
            return;
        }
        stack[++top] = num;
    }
    //出栈
    public int pop(){
        if(isEmpty()){
            throw new RuntimeException("栈中没有数据");
        }
        return stack[top--];
    }

    //显示栈中所有数据
    public void list(){
        if(isEmpty()){
            System.out.println("栈中没有数据");
            return;
        }
        for(int i = top; i >= 0; i--){
            System.out.printf("stack[%d] = %d
",i,stack[i]);
        }
    }
    //判断是不是字符
    public boolean isOper(int oper){
        return oper == "+" || oper == "-" || oper == "*" || oper == "/";
    }
    //获取栈顶元素
    public int getHead(){
        return stack[top];
    }
    //计算

    /**
     *
     * @param num1 第一个是num1
     * @param num2 第二个是num2
     * @param oper 第三个是运算符
     * @return 计算结果
     */
    public int cal(int num1,int num2,int oper){
        int result = 0;
        switch(oper){
            case "+":
                result = num1 + num2;
                break;
            case "-":
                result = num2 - num1;
                break;
            case "*":
                result = num1 * num2;
                break;
            case "/":
                result = num2 / num1;
                break;
        }

        return result;
    }

    //判断符号的优先级，每个符号的优先级由我们自己定义设置
    public static int priority(int oper){
        if(oper == "*" || oper == "/"){
            return 1;
        }else if(oper == "+" || oper == "-"){
            return 0;
        }else{
            return -1;
        }
    }
}

//Calculator类实现
public class Calculator {
    public static void main(String[] args) {
        //要计算的算式
        String express = "7*8-8+2*3+4-7";
        //定义两个栈，一个用来保存数，一个用来保存符号
        ArrayStack2 numStack = new ArrayStack2(10);
        ArrayStack2 operStack = new ArrayStack2(10);
        int index = 0;//用于遍历表达式的索引
        int num1 = 0;//用于保存弹出来的数1
        int num2 = 0;
        int result = 0;//保存结果
        int oper = 0;//保存符号
        char ch = " ";//扫描每次得到的数据
        //1.需要先扫描字符串，可以通过一个 index 变量来辅助扫描

        while(true){
            ch = express.substring(index,index+1).charAt(0);
            //判断是不是符号
            if(numStack.isOper(ch)){
              //当我们遍历的数据是符号的情况
                if(operStack.isEmpty()){
                    //查看栈是否为空，为空，直接将符号添加
                    operStack.push(ch);
                }else{
                    //进行比较添加,如果当前符号的优先级大于，栈顶元素的优先级，直接添加，否则
                    //弹出数栈两个数进行计算，弹出符号栈符号，进行运算，将结果加入数栈，
                    // 然后再将现在符号加入符号栈
                    if(ArrayStack2.priority(ch) > ArrayStack2.priority(operStack.getHead())){
                        //大于情况，直接添加
                        operStack.push(ch);
                    }else{
                       //小于或者等于情况
                        num1 = numStack.pop();
                        num2 = numStack.pop();
                        oper = operStack.pop();
                        result = numStack.cal(num1,num2,oper);
                        numStack.push(result);
                        operStack.push(ch);
                    }

                }
            }else{
               //当我们遍历的数据是数字的时候
                numStack.push(ch - 48);//这里一定要减48，不减48添加的是对应数字的asci码的对应数字
            }
            index++;
            if(index >= express.length()){
                break;//扫描完成
            }
        }
        //当扫描完毕时，从符号栈，数栈弹出数据进行计算
        while(true){
            num1 = numStack.pop();
            num2 = numStack.pop();
            oper = operStack.pop();
            result = numStack.cal(num1,num2,oper);
            numStack.push(result);
            if(operStack.isEmpty()){//符号栈全部弹出以后，计算结束
                break;
            }
        }
        //当遍历完成以后，数栈中的数据就是计算结果
        System.out.printf("%s = %d
",express,numStack.pop());
    }
}

hmoban主题是根据ripro二开的主题，极致后台体验，无插件，集成会员系统
自学咖网 » 数据结构与算法(二)

wen 普通

分享到：

双向链表

单向链表的缺点

双向链表的思路分析

代码实现

单向环形链表-Josephu 问题

应用场景-约瑟夫问题

单向环形链表介绍

约瑟夫问题示意图

创建环形链表的思路图解

环形链表添加思路

遍历环形链表

环形链表实现代码

出圈思路分析

出圈代码实现

栈

栈快速入门

计算器需求

栈介绍

栈的应用场景

数组模拟栈

链表模拟栈

综合计算器

什么是中缀表达式

思路分析

代码实现

wen 普通

相关推荐