栈与队列（含单调栈与单调队列）

栈

算法思路

栈（(stack)）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。 —-摘自 百度百科

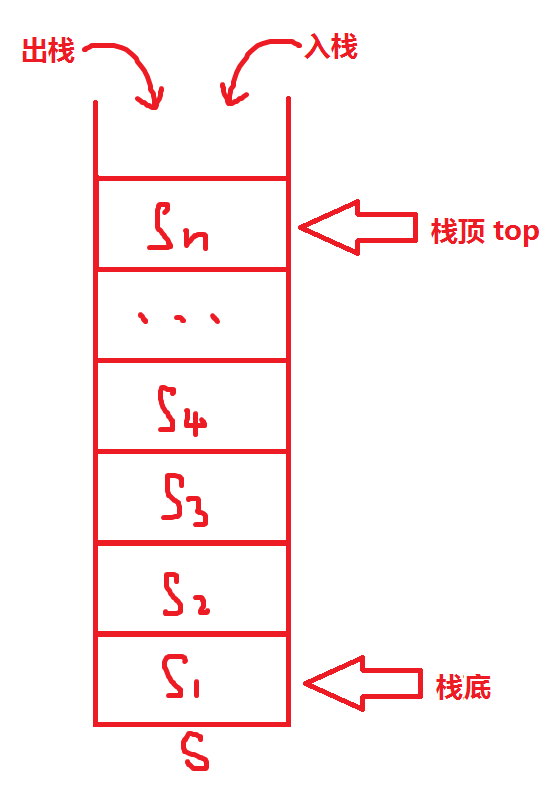
由上述资料可知，栈是一个“先进后出”的数据结构。是只能在栈顶插入和删除的数据结构。如图，支持进栈（(push)）和出栈（(pop)）两种操作。由于只能从一端进栈，一端出栈，所以任一元素，如上图中的(s_2)，必须得在比它后进栈的(s_3sim s_n)（(s_n)即(s_{top})）都出栈以后才能出栈，换句话说，先进来的元素必须等后进来的元素都出栈后才能出栈，故栈被称为“先进后出（(FILO)）表”。

代码片段

进栈

进栈很简单，只需要将栈顶上移一格，然后在新的一格中放入元素即可。

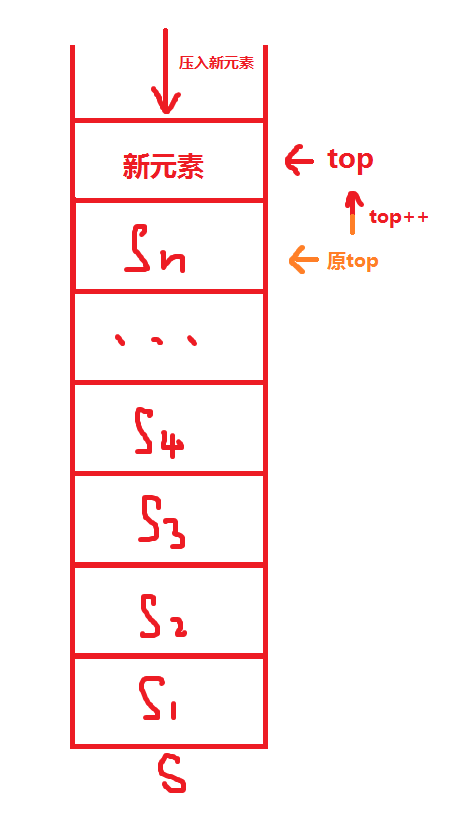
void push(int x){
  s[++top]=x;
}

出栈

出栈也很简单，只需要将栈顶下移一格即可，且不需要替换，因为如果有元素进栈需占用此格时会将它替换。

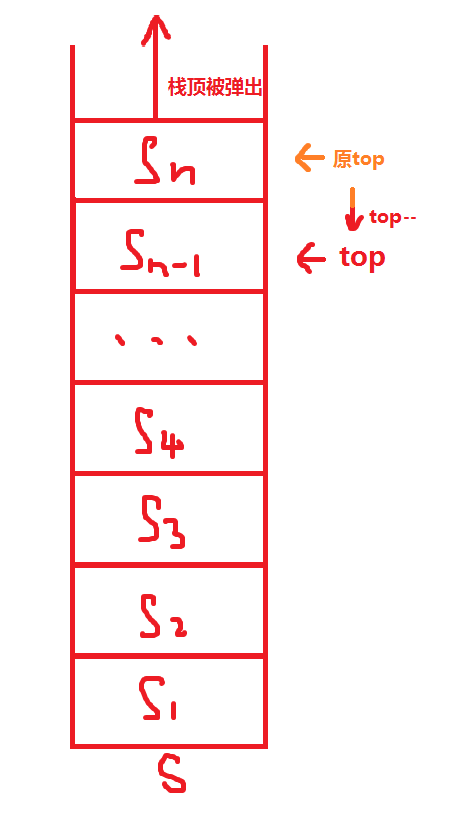
void pop(){
  top--;
}

例题

P1739 表达式括号匹配

大意

给定一个以(@)结尾的表达式，判断其括号（只有“(”和“)”）是否匹配。
“(()())”，“((()))”匹配，但是“())”，“)()(”不匹配。

思路

如果只判断左右括号的数量的话显然是不行的，因为有很多数据显然过不去，如“)()(”，“())(()”等。
所以，这时候，我们就要使用栈了。逐个读入表达式，若为“(”则入栈（显然此时栈应该为(char)类型），若为“)”则判断，若栈顶为空或为“)”，即不为“(”，说明此时这个右半圆括号没有匹配到左半圆括号，说明不匹配。另外，若最后栈顶不为(0)，说明还有剩下的括号没被匹配，也是不合法的。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
char a[260],s[260];
int top=0;
int main(){
	cin>>a;
	for(int i=0;i<strlen(a);i++){
		if(a[i]=="("){
			s[++top]=a[i];
		}else if(a[i]==")"){
			if(a[i]==")"&&s[top]=="("){
				top--;
			}else{
				cout<<"NO";
				return 0;
			}
		}
	}
	if(top==0){
		cout<<"YES";
	}else{
		cout<<"NO";
	}
	return 0;
}

P1449 后缀表达式求值

科普

逆波兰式（(Reverse Polish notation)，(RPN)，或逆波兰记法），也叫后缀表达式（将运算符写在操作数之后）。
一个表达式(E)的后缀形式可以如下定义：
（1）如果(E)是一个变量或常量，则E的后缀式是(E)本身。
（2）如果(E)是(E1 op E2)形式的表达式，这里(op)是任何二元操作符，则E的后缀式为(E1″E2″ op)，这里(E1″)和(E2″)分别为(E1)和(E2)的后缀式。
（3)如果(E)是((E1))形式的表达式，则(E1)的后缀式就是(E)的后缀式。
如：我们平时写(a+b)，这是中缀表达式，写成后缀表达式就是：(ab+)。
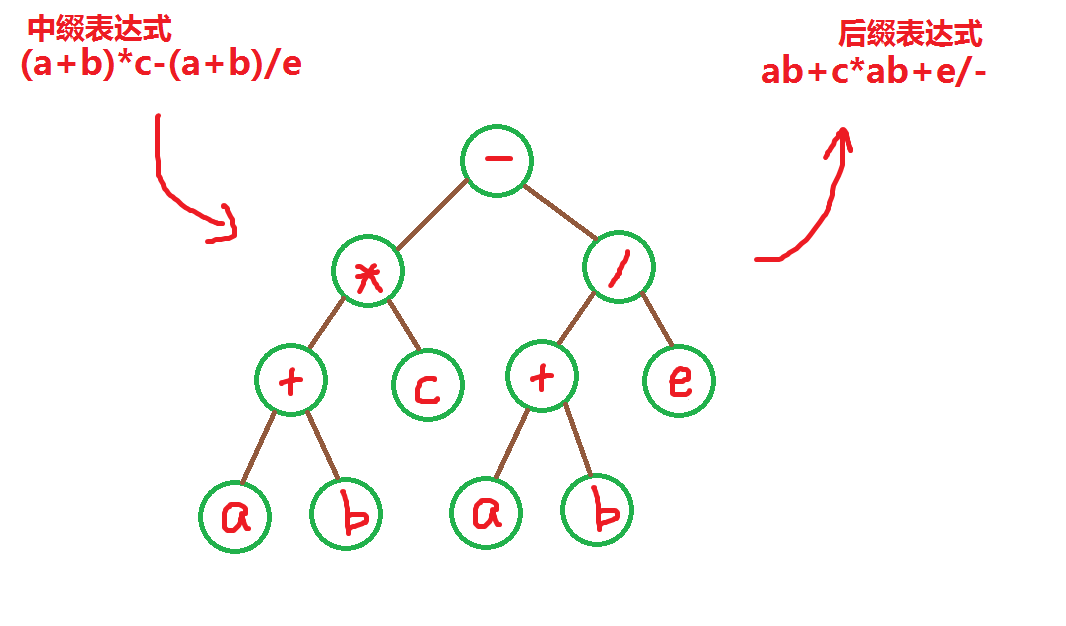
((a+b)*c-(a+b)/e)的后缀表达式为：
((a+b)*c-(a+b)/e)
→(((a+b)*c)((a+b)/e)-)
→(((a+b)c*)((a+b)e/)-)
→((ab+c*)(ab+e/)-)
→(ab+c*ab+e/-)

这里用树解释上述样例：
首先我们构建上述表达式的树，使得树的中序遍历为表达式（因为我们写的是中缀表达式。若想将前缀表达式，即波兰式 变为树，则需构建树让其前序遍历为表达式即可），那么，这棵树的后序遍历就是逆波兰式。

大意

给出后缀表达式，输出其值。

思路

一个个读入后缀表达式，遇到数字进栈，遇到符号计算栈顶和栈顶后一位的元素，最后输出栈顶即可。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int s[260],top=1;
char x;
int main(){
	while(x!="@"){
		x=getchar();
		if(x=="."){
			top++;
		}else{
			if(x>="0"&&x<="9"){
				s[top]=s[top]*10+(x-"0");
			}
			if(x=="+"){
				top--;
				s[top-1]+=s[top];
				s[top]=0;
			}else if(x=="-"){
				top--;
				s[top-1]-=s[top];
				s[top]=0;
			}else if(x=="*"){
				top--;
				s[top-1]*=s[top];
				s[top]=0;
			}else if(x=="/"){
				top--;
				s[top-1]/=s[top];
				s[top]=0;
			}else if(x=="@"){
				break;
			}
		}
	}
	cout<<s[--top];
	return 0;
}

队列

算法思路

栈是一端进和出的数据结构，对应地，队列是一端进、另一端出的数据结构。

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。 ——摘自 百度百科

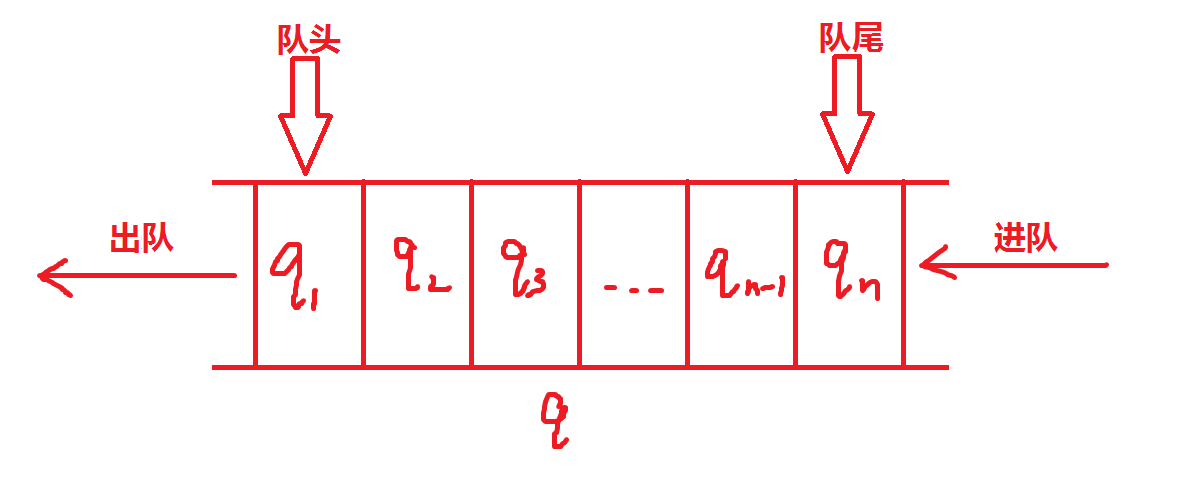
与栈类似，不多赘述。

单调栈

算法思路

顾名思义，单调栈是一种栈内元素具有单调性的栈。也就是说，我们将数列内的元素入栈，且要让栈内元素单调递增或单调递减。维护这样一个栈也很简单（以下假设维护单调递增的单调栈），我们将栈内的元素(s_i)表示为数列(a)中的元素的下标，也就是说，当你在看到栈内有一个元素(x)时，它表示的不是数字(x)，而是表示(a)数组中的元素(a_x)，这一点需要特别注意。入栈时，如果栈顶元素表示的值大于加入的值（即(a_{s_{top}}>a_x)，(x)表示加入的元素，显然为(a)数组中的元素下标），那么将(top–)，即把栈顶踢出去。因为加进来的(x)，即代表的(a_x)，已经小于栈顶了，而我们要维护单调递增的栈，所以若(x)直接加入会破坏单调性，故要让栈顶出栈。等到所有的要踢出栈顶(top)都被踢出后（即现在的栈顶(top)符合(a_{s_{top}}<a_x)），就可以将(x)入栈了。
那么，单调栈有什么作用呢？显然，你可以维护一个单调递增的栈，通过按顺序一个个入栈序列中的元素，可以求出长度为(n)的序列(a)中的前(k)个元素的最小值（(0<kle n)）。因为栈是单调递增的，所以按顺序加入前(k)个元素后，栈顶一定是前(k)个数中的最小值。但是，你显然可以不用单调栈来解决这一个非常基础的问题。单调栈的主要作用之一就是求出序列中每个数右（或左）边第一个比它大（或者小）的数（详情请见例题1）。

例题

P5788 【模板】单调栈 & P2947 [USACO09MAR]Look Up S

大意

求出序列中每个数右边第一个比它大的数。

思路

维护一个单调递减的栈，那么，对于每一个元素，让它被踢出去的那个元素一定是第一个比它大的元素。（建议自己画图好好分析一下）。

代码

#include<iostream>
#include<cstdio>
#define maxn 100005
using namespace std;
int n,a[maxn];
int s[maxn],top=0;
int ans[maxn];
void push(int x){
	while(a[s[top]]<a[x]&&top>0){
		ans[s[top]]=x;
		top--;
	}
	s[++top]=x;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
	}
	s[++top]=1;
	for(int i=2;i<=n;i++){
		push(i);
	}
	for(int i=1;i<=n;i++){
		printf("%d ",ans[i]);
	}
	return 0;
}

P1901 发射站

大意

有(n)个发射站，每一个发射站有一个高度(h_i)和能量值(v_i)，对于每个发射站(i)，它左边和右边第一个比它高的发射站都可以接收到它发出的信号（即累计值加上(v_i)），求每个信号塔累计的能量值总和的最大值。

思路

同上两题，只不过要加两次。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 1000005
using namespace std;
int n,a[maxn],v[maxn];
int s[maxn],top=0;
int ans[maxn];
void push(int x){
	while(a[s[top]]<a[x]&&top>0){
		ans[x]+=v[s[top]];
		top--;
	}
	s[++top]=x;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&a[i],&v[i]);
	}
	s[++top]=1;
	for(int i=2;i<=n;i++){
		push(i);
	}
	memset(s,0,sizeof(s));
	top=0;
	s[++top]=n;
	for(int i=n-1;i>=1;i--){
		push(i);
	}
	int mmax=-1;
	for(int i=1;i<=n;i++){
		mmax=max(mmax,ans[i]);
	}
	printf("%d ",mmax);
	return 0;
}

P2422 良好的感觉

大意

有一长为(n)的序列(a)，定义某区间([l,r])的值(comfort_{l,r} = minlimits_{i=l}^{r}{a_i} imes sumlimits_{i=l}^{r}{a_i})，求(max(comfort_{i,j})(0 < ile jle n))。

思路

可以想象，枚举每个区间需要耗费大量的时间，这很可能会使我们(TLE)。我们不妨枚举(min(i,j))，显然我们只需要枚举(n)次，因为我们可以从(1)到(n)枚举(i)，计算以(a_i)为最小值的区间中的最大(comfort_{l,r})，因为(a_i ge 1)，所以我们只要让区间越大越好，所以我们需要枚举的区间即为从(a_i)开始，左右两边各延伸到离它最近的比它小的两个位置（不包括这两个比它小的值）（因为这样就可以保证区间内没有小于(a_i)的数，即(a_i)为区间内最小值，且区间最大），计算所有的(a_i)计算的区间的和乘(a_i)（即以(a_i)为最小值的最大(comfort)值）的最大值即为所求最大值。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 100005
using namespace std;
int n,a[maxn];
long long pre[maxn];
int le[maxn],ri[maxn];
int s[maxn],top=0;
void pushr(int x){
	while(a[s[top]]>a[x]&&top>=0){
		ri[s[top]]=x;
		top--;
	}
	s[++top]=x;
}
void pushl(int x){
	while(a[s[top]]>a[x]&&top>=0){
		le[s[top]]=x;
		top--;
	}
	s[++top]=x;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		pre[i]=pre[i-1]+a[i];
	}
	s[++top]=1;
	for(int i=2;i<=n;i++){
		pushr(i);
	}
	memset(s,0,sizeof(s));
	top=0;
	s[++top]=n;
	for(int i=n-1;i>=1;i--){
		pushl(i);
	}
	for(int i=1;i<=n;i++){
		ri[i]=ri[i]==0?n+1:ri[i];
	}
	long long ans=-1;
	for(int i=1;i<=n;i++){
		ans=max(ans,(long long)(a[i]*(pre[ri[i]-1]-pre[le[i]])));
	}
	printf("%lld",ans);
	return 0;
}

单调队列

算法思路

我们刚才讲到，单调栈可以算出一组数据中前(k)个数据中的最值（虽然不用单调栈更简单易懂），那么，如何计算一组数据中任意连续(k)个数据的最值呢（(0<kle n)）？这时，我们就要用到单调队列了（注：用线段树也可以）。
单调队列相当于单调栈，但是它在队头也可以进行删除操作（即(head++)）。以上述题目（即例题(1)）为例，我们只要控制这个单调队列的队头始终满足在所求范围内即可。更详细的思路见例题(1)。

例题

P1886 滑动窗口 /【模板】单调队列

大意

有一串长(n)的序列，有一个长(m)的窗口从(1)到(n-m+1)滑动（(0<m<=n)），求每滑动一次窗口的最值。

思路

模板题。
维护队列(q)（当然能用(STL)），（这里讲最大值的做法，最小值同理）每次加入一个元素，从队尾把小于此元素的从队尾出队（因为当前的元素已经比它大了，且窗口向右滑动，所以它必定不可能再一次成为最大值），从队首将不在范围内的元素从队首出队，这时队首即为最大值。
代码中，先将前(k-1)个元素入队，然后循环(i)（(kle ile n)），枚举队尾，用(push)函数从队尾插入，同时从队头删去(i-k+1)之前的元素，即已经不在滑动窗口内的元素，输出队头。

代码

#include<iostream>
#include<cstdio>
#define maxn 1000005
using namespace std;
int n,k;
int a[maxn];
int q1[maxn],q2[maxn],h1=1,t1=0,h2=1,t2=0;//q1维护最大值,q2维护最小值 
int ans1[maxn],ans2[maxn];
void push1(int x,int l){
	while(t1>=h1&&a[x]>a[q1[t1]]){
		t1--;
	}
	q1[++t1]=x;
	while(t1>=h1&&q1[h1]<l){
		h1++;
	}
}
void push2(int x,int l){
	while(t2>=h2&&a[x]<a[q2[t2]]){
		t2--;
	}
	q2[++t2]=x;
	while(t2>=h2&&q2[h2]<l){
		h2++;
	}
}
int main(){
	scanf("%d%d",&n,&k);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
	}
	q1[++t1]=1;
	q2[++t2]=1;
	for(int i=2;i<=k;i++){
		push1(i,-1);
		push2(i,-1);
	}
	ans1[1]=q1[h1];
	ans2[1]=q2[h2];
	for(int i=k+1;i<=n;i++){
		push1(i,i-k+1);
		push2(i,i-k+1);
		ans1[i-k+1]=q1[h1];
		ans2[i-k+1]=q2[h2];
	}
	for(int i=1;i<=n-k+1;i++){
		printf("%d ",a[ans2[i]]);
	}
	printf("
");
	for(int i=1;i<=n-k+1;i++){
		printf("%d ",a[ans1[i]]);
	}
	return 0;
}

注

双倍经验（只需求最大值）：P2032 扫描

P2629 好消息，坏消息

大意

给定一个环，问从任意元素开始累加，有多少种情况使得累加时总和(tot)恒大于等于(0)。

思路

断环成链，维护单调队列和前缀和(pre_i)，若某一长度为(n)的序列(isim i+n-1)的最小值减(pre_{i-1})大于零的话即可行。

代码

#include<iostream>
#include<cstdio>
#define maxn 1000005
using namespace std;
int n,k;
int a[maxn*2],pre[maxn*2];
int q[maxn],h=1,t=0;
int ans[maxn];
void push(int x,int l){
	while(t>=h&&pre[x]<pre[q[t]]){
		t--;
	}
	q[++t]=x;
	while(t>=h&&q[h]<l){
		h++;
	}
}
int main(){
	scanf("%d",&n);
	k=n;
	n*=2;
	for(int i=1;i<=k;i++){
		scanf("%d",&a[i]);
		a[i+k]=a[i];
	}
	for(int i=1;i<=n;i++){
		pre[i]=pre[i-1]+a[i];
	}
	q[++t]=1;
	for(int i=2;i<=k;i++){
		push(i,-1);
	}
	ans[1]=q[h];
	for(int i=k+1;i<n;i++){
		push(i,i-k+1);
		ans[i-k+1]=q[h];
	}
	int tot=0;
	for(int i=1;i<=n-k;i++){
		if(pre[ans[i]]-pre[i-1]>=0){
			tot++;
		}
	}
	printf("%d",tot);
	return 0;
}

单调队列优化DP

例题

P1725 琪露诺

大意

有一串长度为(n+1)的序列(a)，从(0)出发，在某个节点(i)能走到(i+lsim i+r)的任意位置，(tot)累加当前位置的(a_i)，求离开时的最大(tot)值（(i+r>n)代表从(i)节点能离开）。

思路

显然此题暴力代码复杂度为(O(N^2))，(f_i=maxlimits_{j=max(0,i-r)}^{i-l}{f_j}(l<=i<=n))，那么，我们只要开一个单调队列求前文的(max(f_j))即可。

代码

（细节很多）

#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 1000005
#define INF 0x3f
using namespace std;
int n,l,r;
int a[maxn];
int q[maxn],h=1,t=0,maxx[maxn];
int f[maxn];
void push(int x,int l){
	while(f[x]>f[q[t]]&&h<=t){
		t--;
	}
	while(q[h]<l&&h<=t){
		h++;
	}
	q[++t]=x;
}
void clear(int l){
	while(q[h]<l&&h<=t){
		h++;
	}
}
int main(){
	scanf("%d%d%d",&n,&l,&r);
	memset(f,0x80,sizeof(f));
	memset(q,-1,sizeof(q));
	for(int i=0;i<=n;i++){
		scanf("%d",&a[i]);
	}
	f[0]=0;
	push(0,-1);
	for(int i=l;i<=n;i++){
		if(i-l>=l){
			push(i-l,max(0,i-r));
		}else{
			clear(max(0,i-r));
		}
		if(q[h]==-1){
			f[i]=f[maxn-1]+a[i];
		}else{
			f[i]=f[q[h]]+a[i];
		}
//		for(int j=i-l;j>=max(0,i-r);j--){
//			f[i]=max(f[i],f[j]+a[i]);
//		}
	}
	int ans=-INF;
	for(int i=n;i>=n-r+1;i--){
		ans=max(ans,f[i]);
	}
	printf("%d",ans);
	return 0;
}

P2627 Mowing the Lawn G

大意

有一个长度为(n)的序列，选出若干个元素，使得选出的元素没有连续超过(k)个的（(0<k<=n)），求选出元素的和的最大值。

思路

选出的数的和的最大值可以转换成删去的数的和的最小值。

代码

#include<iostream>
#include<cstdio>
#define maxn 100005
using namespace std;
long long n,k,a[maxn],f[maxn];
long long q[maxn],h=0,t=0;
long long tot=0;
void push(long long x,long long l){
	while(f[x]<f[q[t]]&&h<=t){
		t--;
	}
	while(q[h]<l&&h<=t){
		h++;
	}
	q[++t]=x;
}
int main(){
	scanf("%lld%lld",&n,&k);
	for(long long i=1;i<=n;i++){
		scanf("%lld",&a[i]);
		tot+=a[i];
	}
	for(int i=1;i<=n;i++){
		f[i]=f[q[h]]+a[i];
		push(i,i-k);
	}
	long long mmin=f[n-k];
	for(long long i=n-k+1;i<=n;i++){
		mmin=min(f[i],mmin);
	}
	printf("%lld",tot-mmin);
	return 0;
}
/*
5 4
1 2 3 4 5
*/

注

双倍经验：P2034 扫描

qzez1926 玉米实验

大意

给定一个(n*n)的矩阵(a)，有(t)次询问，每次询问以((x_i,y_i))为左上角、长宽均为(k)的矩阵中，最大值与最小值的差值是多少。

思路

首先，我们还是显然能得出暴力的代码：
(ans_i = maxlimits_{x=x_i , y=y_i}^{x_i+k-1 , y_i+k-1}{a_{{x},{y}}} – minlimits_{x=x_i , y=y_i}^{x_i+k-1 , y_i+k-1}{a_{{x},{y}}})。
然后，由于(k)是给定的，这让我们想到可以用单调队列优化(max(a_{{x},{y}}))和(min(a_{{x},{y}}))，即预处理矩阵(a)，算出矩阵每一行的长(k)的滑动窗口中的最值，询问时直接查询子矩阵第一列的最值即可。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 1005
#define INF 99999999
using namespace std;
int n,k,t,x,y;
int a1[maxn][maxn],a2[maxn][maxn];
int q1[maxn],q2[maxn],h1=1,t1=0,h2=1,t2=0;
int ans1[maxn][maxn],ans2[maxn][maxn];
void push1(int i,int x,int l){//找最小值 
	while(a1[i][x]<a1[i][q1[t1]]&&h1<=t1){
		t1--;
	}
	q1[++t1]=x;
	while(q1[h1]<l&&h1<=t1){
		h1++;
	}
}
void push2(int i,int x,int l){//找最大值 
	while(a2[i][x]>a2[i][q2[t2]]&&h2<=t2){
		t2--;
	}
	q2[++t2]=x;
	while(q2[h2]<l&&h2<=t2){
		h2++;
	}
}
void doit(int i){
	memset(q1,0,sizeof(q1));
	memset(q2,0,sizeof(q2));
	h1=1;t1=0;h2=1;t2=0;
	q1[++t1]=1;q2[++t2]=1;
	for(int j=2;j<k;j++){
		push1(i,j,-1);
		push2(i,j,-1);
	}
	for(int j=k;j<=n+k;j++){
		push1(i,j,j-k+1);
		push2(i,j,j-k+1);
		ans1[i][j-k+1]=q1[h1];
		ans2[i][j-k+1]=q2[h2];
	}
}
int main(){
	memset(a1,0x3f,sizeof(a1));
	scanf("%d%d%d",&n,&k,&t);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			scanf("%d",&a1[i][j]);
			a2[i][j]=a1[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		doit(i);
	}
//	printf("
");
//	for(int i=1;i<=n;i++){
//		for(int j=1;j<=n;j++){
//			printf("%d ",a2[i][ans2[i][j]]);
//		}
//		printf("
");
//	}
//	printf("
");
	while(t--){
		scanf("%d%d",&x,&y);
		int mmax=-1,mmin=INF;
		for(int i=0;i<k;i++){
			mmax=max(mmax,a2[x+i][ans2[x+i][y]]);
			mmin=min(mmin,a1[x+i][ans1[x+i][y]]);
		}
		printf("%d
",mmax-mmin);
	}
	return 0;
} 
/*
5 3 2
5 1 2 6 3
1 3 5 2 7
7 2 4 6 1
9 9 8 6 5
0 6 9 3 9
2 1
1 2
*/