PHP最高效率的将一个正整数扩大一千倍
方案制定
如何最高效率的将一个正整数扩大一千倍?
当这个问题被抛给人脑的时候,接受过优秀的九年义务教育的我们稍加思索就能给出一个调皮而又不失大师风范的答案:添三个零就行了~
但是当这个问题交给程序员用代码解决的时候,问题就要从编程的角度去考虑。我作为phper第一时间想到的方案分别是
-
方案1:在数字末尾粘连字符串 “000”
-
方案2:将原数字简单的乘以 1000
当我把这个问题丢给我的朋友的时候,他告诉我:
方案1肯定不行!你应该采用方案2,但是如果你足够鸡贼的话,你应该采用正整数 X 1024 - 正整数 X 24!
因为计算机是二进制,当你告诉他要乘以1000的时候,他会进行正整数 X 512 + 正整数 X 256 + 正整数 X 128 + 正整数 X 128 + 正整数 X 64 + 正整数 X 32 + 正整数 X 8,一直累加到凑齐 正整数的 1000 倍 为止。而运算2的10次方要比那一串加号更快接近结果。
【推荐学习:PHP视频教程】
实践出真知
大佬的这段话很快打动了我。为了践行大佬的真知,证明大佬的阐述对我犹如醍醐灌顶般点醒梦中人,我迅速写出了一小段方法,将一个随机正整数扩大1000倍的算法用三种不同的方法分别跑 一千万次,查看各个方法运行的效率(使用框架:laravel)
// 图表内容
$headers = ['次数', '方案1:拼接法', '方案2:乘1000', '方案3:乘以 1024'];
$data = [
[0=>'第一次'],
[0=>'第二次'],
[0=>'第三次']
];
// 每个方法执行三次
for ($count = 0; $count < 3; $count ++) {
// 生成变量名 : plan1start1
$start = Carbon::now()->getPreciseTimestamp();
for ($i = 0; $i < 10000000; $i ++)
{
$integer = rand(1, 999);
$result = (int)($integer . '000');
}
$end = Carbon::now()->getPreciseTimestamp();
$data[$count][] = ($end - $start)/1000000 . '秒';
}
for ($count = 0; $count < 3; $count ++) {
$start = Carbon::now()->getPreciseTimestamp();
for ($i = 0; $i < 10000000; $i ++)
{
$integer = rand(1, 999);
$result = $integer * 1000;
}
$end = Carbon::now()->getPreciseTimestamp();
$data[$count][] = ($end - $start)/1000000 . '秒';
}
for ($count = 0; $count < 3; $count ++) {
$start = Carbon::now()->getPreciseTimestamp();
for ($i = 0; $i < 10000000; $i ++)
{
$integer = rand(1, 999);
$result = $integer * 1024 - $integer * 24;
}
$end = Carbon::now()->getPreciseTimestamp();
$data[$count][] = ($end - $start)/1000000 . '秒';
}
$this->table($headers, $data);
将这段代码运行多次后均得到一个较为稳定的结果:
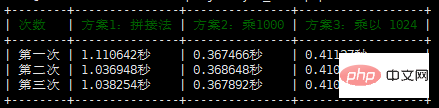
看到这个结果,大大的疑问重新占领了我小小的脑瓜。乘以 1024 再减去 乘以 24 反而比直接乘以 1000慢一些。当我拿着这个结果去寻找大佬解决疑惑时,得到了他这样的回答:
平时工作不够多是不是?还有空做这种试验?
对试验结果的思考
暗戳戳鄙夷他一把,顺便把他在我心中的地位从大佬降格为我的某个不愿透露姓名的普通朋友。我继续了对这件事请的思考。
在正整数后面拼接字符串 ‘000’,要把这个正整数转换为字符串,然后拼接字符串 ‘000’,之后再转回正整数。计算的复杂程度远超正整数的直接计算,时间上明显劣于后者,这点经过验证也毋庸置疑。
但是我的某个不愿透露姓名的豆豆同学对二进制计算模式解释的同样头头是道。我学习的是解释型语言 php,这意味着有一群对代码理解达到骨灰级的玩家在我看不到的地方对php进行了大量的算法优化。而豆豆同学学习的是编译型语言 C++。是不是这种解释型语言的不同点,导致了本次运算结果的不同?

