并查集

在一张图中，我们常常会遇到判断两个点是否在同一个连通块上，此时，我们若采用朴素而低效的dfs的方法，就有超时的危险，于是我们引入了一种更加实用的算法——并查集。

父节点表示法

首先，我们来了解一个树的存储方法：父节点表示法。

因为每个节点只有唯一父节点，于是我们用 parent[i] 来表示节点 (i) 的父节点。特别地，我们规定在此时根节点的父节点是其本身。

比如下面这棵树：

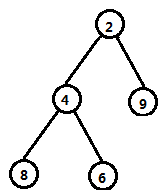
用父节点表示法表示出来就是

tree[2]=2
tree[4]=2
tree[8]=4
tree[6]=4
tree[9]=2

并查集的原理

有了父节点表示，我们就可以开始搞定并查集了。

模板题

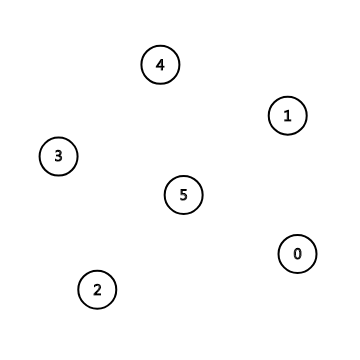
首先，我们的并查集一开始是一个森林，每个节点独立作为一棵树。

接着，我们来进行合并操作，我们先来合并 (0,1) 两个节点，于是我们把节点 (0) 连到 (1) 上，就变成了下面这样：

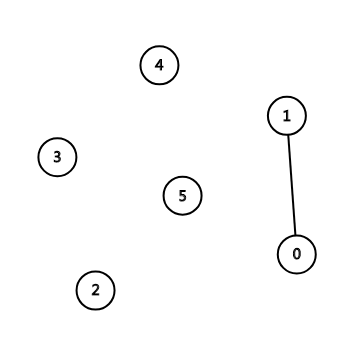
用代码表示就是tree[0]=1

但如果我们要合并的两个节点不是根节点呢？

这个简单，我们只要向上找到根节点，再合并根节点就行了。

接着进行查询，我们依然查询 (0,1) 两个节点，这时只需要一直向上查找至根节点，看两个根节点是否相同就行了。

如何找根节点呢，我们在上面提到过，根节点的父节点等于本身，于是我们就可以写出这样的代码。

int find_root(int u){
    return parent[u]==u?find_root(parent[u]):u;
}

优化

我们看到，对于一个并查集，如果我们的合并使其退化成一条链或近似于链的状态会使效率大幅降低，于是需要一定方法优化。

首先，我们想会使效率降低的原因，主要是因为需要一个个找，这让我们想到类似找LCA的倍增的做法，但与此同时又会让合并的时间复杂度剧增，因为每次合并都相当于要做一次dfs。

似乎没啥好方法了？

这时候一个非常机智的想法出现了：路径压缩。

我们知道，我们在做并查集的时候并不关心到底这棵树是怎样的，我们只要保证合并完了以后两棵树确实在一起就行了。

于是我们想到，既然我们不关心树的结构，那我们把树破坏掉呗，反正是找根节点，那我们干脆在 find_root() 的时候，直接将子节点连到根节点上去，并且把沿途的节点也连接到根节点上去，于是我们的find_root就可以这么写了

int find_root(int u){
    return parent[u]==u?parent[u]=find_root(parent[u]):u;
}

在这种情况下，单次查询的时间复杂度为(O(log n))

最后，附上模板题AC代码

#include<iostream>
#include<cstring>
using namespace std;
int parent[200000];
int root(int i){
	if(parent[i]==i){return i;}
	return parent[i]=root(parent[i]);
}
int main(){
	int n,m;
	cin>>n>>m;
	for(int i=0;i<=n;++i)parent[i]=i;
	int x,a,b;
	for(int i=0;i<m;++i){
		cin>>x>>a>>b;
		if(x==1)parent[root(a)]=root(b);
		if(x==2){
			if(root(a)==root(b))cout<<"Y"<<endl;
			else cout<<"N"<<endl;
		}
	}
	return 0;
}