数据结构与算法——红黑树的实现
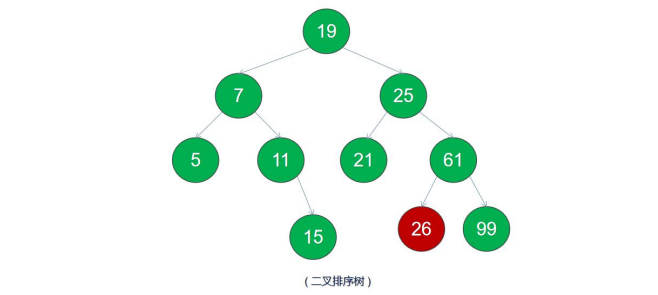
有了二叉搜索树为什么还要红黑树,以下面几个例子举例,如下面的二叉树可以达到很好的搜索效果
| 5 | 7 | 11 | 15 | 19 | 21 | 25 | 26 | 61 | 99 |
再看下面这棵树,我们将下面的数据按从左至右的顺序构造一棵二叉搜索树
| 15 | 13 | 16 | 11 | 9 | 7 | 5 | 3 |
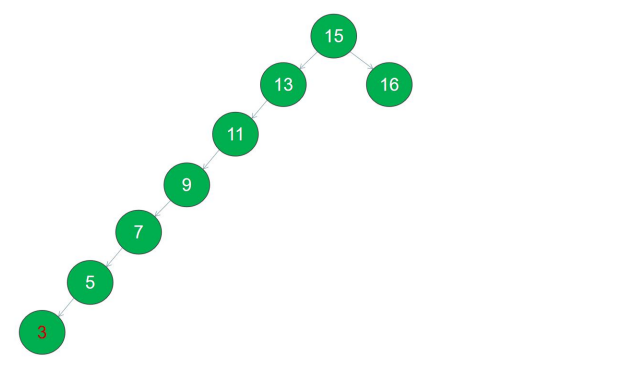
按照之前我们二叉搜索树构建构建的方式,我们将得到下面这样一棵树:
如果找值为 3 的节点,9 个节点需要比较的次数是 7 次,同样的数据,如果我们按照以下顺序构造一棵二叉排序树:
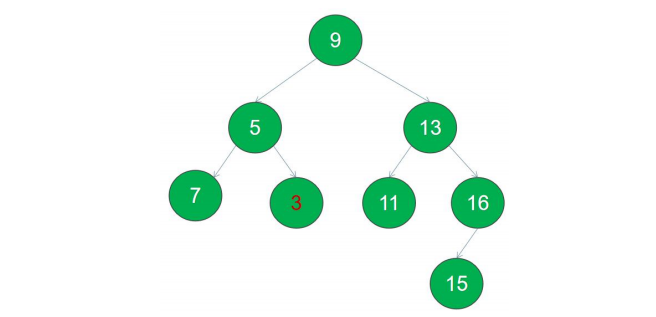
| 9 | 5 | 13 | 7 | 3 | 11 | 16 | 15 |
则查找值为 3 的节点,9 个节点需要比较的次数是 3 次,两者之所以达到了如此之大的差距,原因是第一棵树左右不够平衡,导致出现比较极端的情况。
解决方案: 红黑树
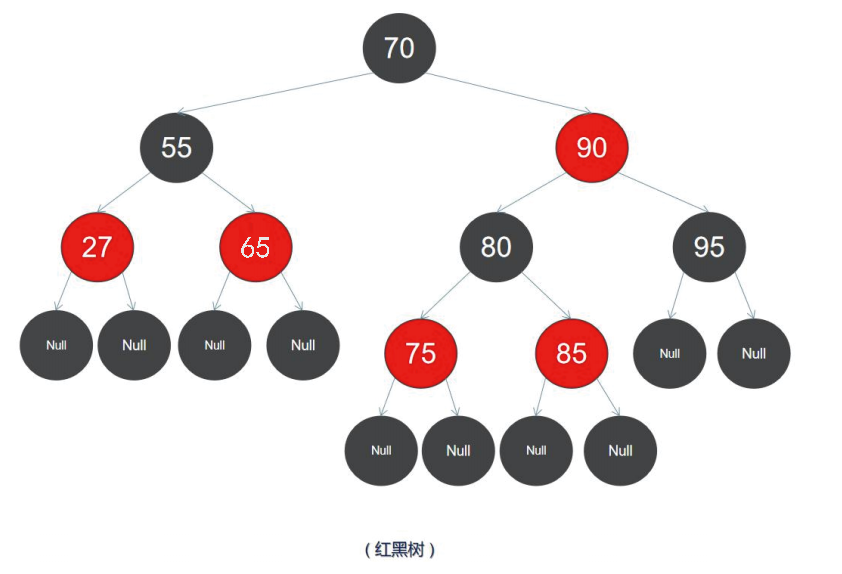
红黑树每个节点都带有颜色属性(颜色为红色或黑色)的自平衡二叉查找树,满足下列性质:
红黑树是一种自平衡二叉查找树,从下面红黑树的图可以看到,根结点右子树显然比左子树高,但左子树和右子树的黑结 点的层数是相等的,也即任意一个结点到到每个叶子结点的路径都包含数量相同的黑结点。所以我们叫红黑树这种平衡为 黑色完美平衡。
1 它是一个自平衡二叉搜索树,满足二叉搜索树的条件;
2 节点是红色或黑色;
3 根节点是黑色;
4 所有叶子节点都是黑色;
5 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节 点。)
6 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
以上例数组为例构建红黑树:
| 15 | 13 | 16 | 11 | 9 | 7 | 5 | 3 |
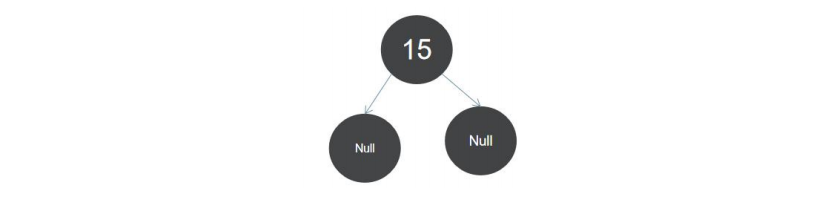
第一步:使用第一个元素 15 创建根节点,根节点一定是黑色,如图:
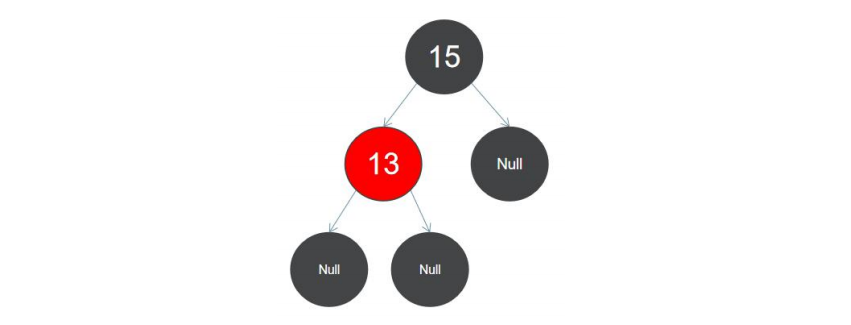
第二步:将 13 加入到红黑树,按照二叉搜索树的规则,13 应插入到 15 的左子节点上面,此时插入红色节点不会破坏红黑 树的平衡,直接插入即可,如图:
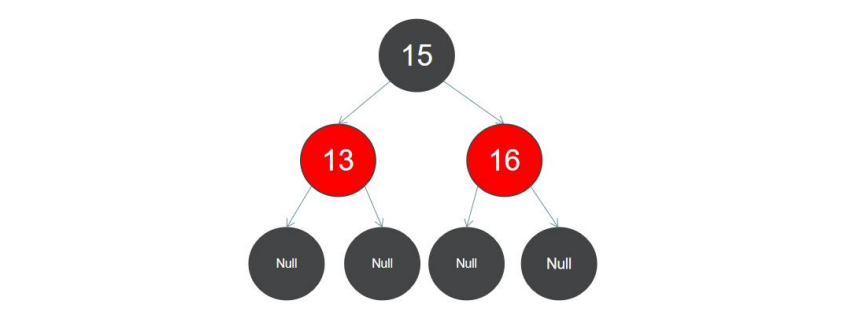
第三步:将 16 加入到红黑树,16 应插入到 15 的右子节点上面,此时插入红色节点不会破坏红黑树的平衡,直接插入即 可,如图所示:
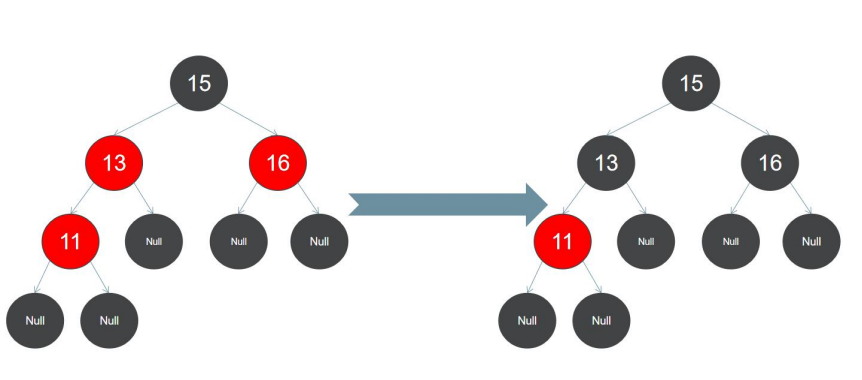
第四步:将 11 加入到红黑树,11 应插入到 13 的左子节点上面,此时继续插入红色节点会破坏红黑树的平衡规则,红色 节点下必须是一对黑色子节点,而插入黑色节点也违背了规则 5(从任一节点到其每个叶子的所有简单路径都包含相同数 目的黑色节点),所以必须进行如下特殊处理:
1. 将 11 的父节点 13 和叔父节点都设置为黑色
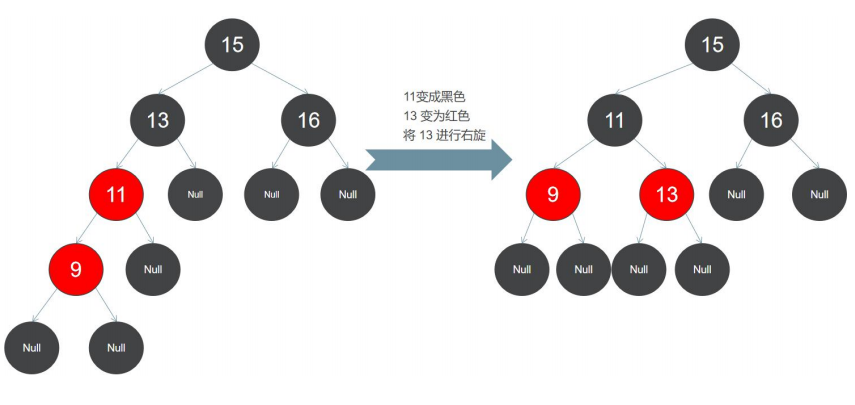
第五步: 将 9 加入到红黑树,9 应插入到 11 的左子节点上面,此时无论插入红色节点或黑色节点都会破坏规则,必须对节 点做挪移处理:
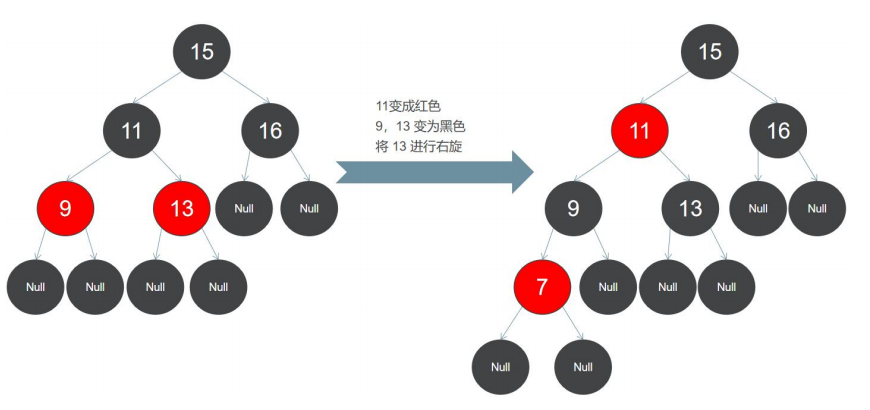
第六步:将 7 加入到红黑树,7 应插入到 9 的左子节点上面,此时无论插入红色节点或黑色节点都会破坏规则,必须对节 点做变色处理:
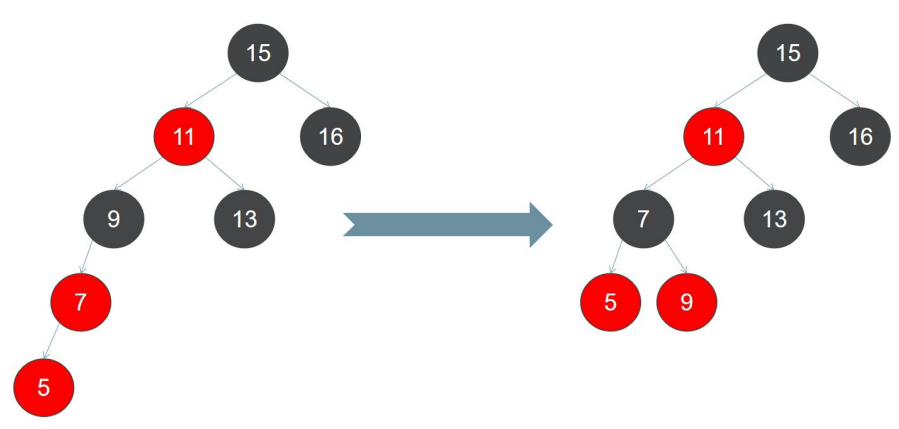
第七步:将 5 加入到红黑树,5 应插入到 7 的左子节点上面,此时无论插入红色节点或黑色节点都会破坏规则,必须对节 点做旋转处理:
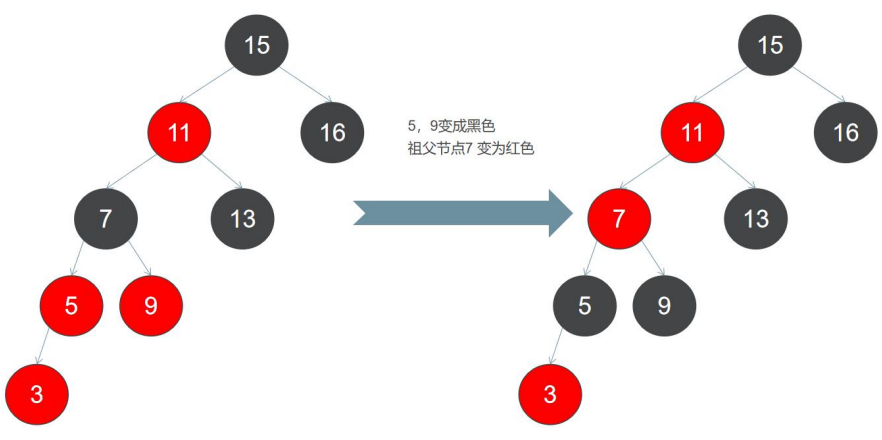
第八步:将 3 加入到红黑树,3 应插入到 5 的左子节点上面,此时无论插入8红9色79节4点3或84黑0色1节1点1都1会破坏规则,我们先对 父节点和叔叔节点做变色处理:
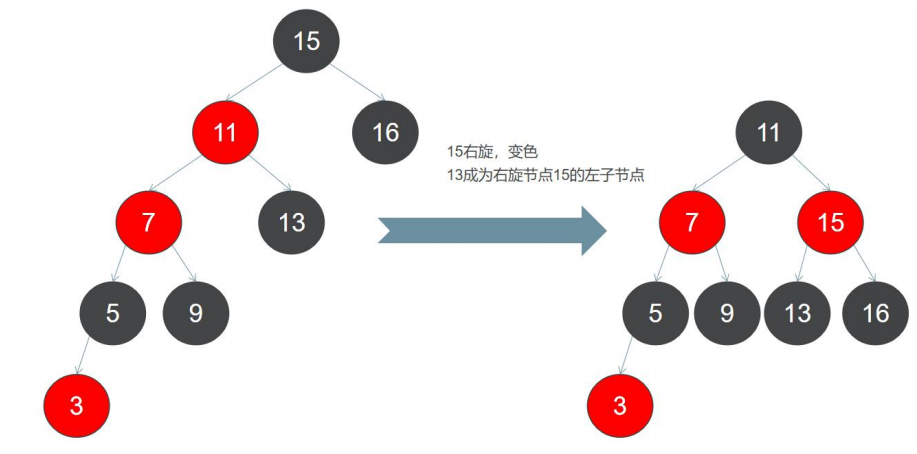
但这样破坏了红色节点 11 必须有两个黑色子节点的规则,因此还得进一步向上调整,此时,要保障红黑树的平衡,我们需 要对根节点进行右旋!
数据结构与算法——红黑树的实现
原文地址:https://www.cnblogs.com/CooCoChoco/p/13970535.html

![数据结构与算法——红黑树的实现
[编程语言教程]](https://www.zixueka.com/wp-content/uploads/2024/01/1706709709-297856c1c591683.jpg)