wen 编程最新 2024-01-31

数据结构与算法（Ⅳ）：树、二叉树、二叉搜索树

树（Tree）

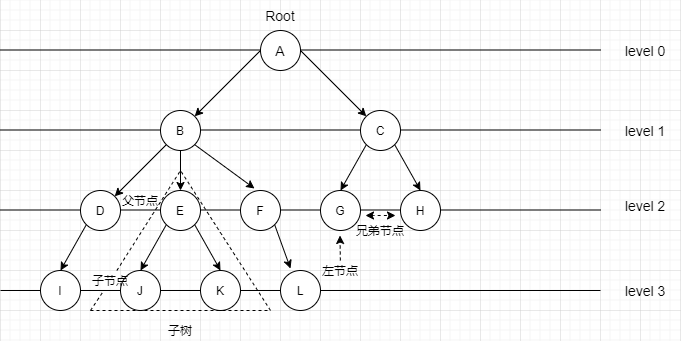
如图，树是非线性表结构，E 节点是 J 节点的父节点，J 节点是 E 节点的子节点。G、H 节点的父节点是同一个节点，所以它们之间互称为兄弟节点。没有父节点的节点叫做根节点，也就是图中的节点 A。没有子节点的节点叫做叶子节点或者叶节点，比如图中的 H、I、J、K、L 都是叶子节点。

除此之外，关于“树”，还有三个比较相似的概念：高度（Height）、深度（Depth）、层（Level）。它们的定义是这样的：

节点的高度 = 节点到叶子节点的最大路径（边数）
节点的深度 = 根节点到这个节点所经历的边的个数
节点的层数 = 节点的深度 + 1
树的高度 = 根节点的高度

二叉树（Binary Tree）

二叉树，顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子节点和右子节点。

图中的树都是二叉树，编号 B 和编号 C 比较特殊：

编号 B 的二叉树中，叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫做满二叉树。

编号 C 的二叉树中，叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫做完全二叉树。

实例代码：

public class TreeNode {
    public int cal;
    public TreeNode left, right;
    public TreeNode (int val) {
        this.val = val;
        this.left = null;
        this.reght = null;
    }
}

二叉树遍历

二叉树遍历经典的方法有三种，前序遍历、中序遍历和后序遍历。其中，前、中、后序，表示的是节点与它的左右子树节点遍历打印的先后顺序。

前序（Pre-order）：打印-左-右
中序（In-order）：左-打印-右
后序（Post-order）：左-右-打印

递归公式：

// 前序遍历的递推公式：
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)

// 中序遍历的递推公式：
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)

// 后序遍历的递推公式：
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r

代码实现：


void preOrder(Node* root) {
  if (root == null) return;
  print root // 此处为伪代码，表示打印root节点
  preOrder(root->left);
  preOrder(root->right);
}

void inOrder(Node* root) {
  if (root == null) return;
  inOrder(root->left);
  print root // 此处为伪代码，表示打印root节点
  inOrder(root->right);
}

void postOrder(Node* root) {
  if (root == null) return;
  postOrder(root->left);
  postOrder(root->right);
  print root // 此处为伪代码，表示打印root节点
}

二叉树遍历时间复杂度：

每个节点最多会被访问两次，所以遍历操作的时间复杂度跟节点的个数 n 成正比，也就是说二叉树遍历的时间复杂度是 O(n)

二叉搜索树（Binary Search Tree）

二叉搜索树，也称二叉查找树、有序二叉树（Ordered Binary Tree）、排序二叉树（Sorted Binary Tree）,是指一棵空树或者具有以下性质的二叉树：

左子树上所有节点的值均小于根节点的值
右子树上所有节点的值均大于根节点的值
以此类推：左右子树也分别是二叉搜索树（这就是重复性）

二叉搜索树中序遍历是升序排列。

二叉搜索树查找操作

先取根节点，如果它等于要查找的数据，那就返回。如果要查找的数据比根节点的值小，那就在左子树中递归查找；如果要查找的数据比根节点的值大，那就在右子树中递归查找。

代码实现：

public class BinarySearchTree {
  private Node tree;

  public Node find(int data) {
    Node p = tree;
    while (p != null) {
      if (data < p.data) p = p.left;
      else if (data > p.data) p = p.right;
      else return p;
    }
    return null;
  }

  public static class Node {
    private int data;
    private Node left;
    private Node right;

    public Node(int data) {
      this.data = data;
    }
  }
}

二叉搜索树插入操作

二叉查找树的插入过程类似查找操作。新插入的数据一般都是在叶子节点上，所以只需要从根节点开始，依次比较要插入的数据和节点的大小关系。

如果要插入的数据比节点的数据大，并且节点的右子树为空，就将新数据直接插到右子节点的位置；
如果不为空，就再递归遍历右子树，查找插入位置。
同理，如果要插入的数据比节点数值小，并且节点的左子树为空，就将新数据插入到左子节点的位置；
如果不为空，就再递归遍历左子树，查找插入位置。

代码实现：

public void insert(int data) {
  if (tree == null) {
    tree = new Node(data);
    return;
  }

  Node p = tree;
  while (p != null) {
    if (data > p.data) {
      if (p.right == null) {
        p.right = new Node(data);
        return;
      }
      p = p.right;
    } else { // data < p.data
      if (p.left == null) {
        p.left = new Node(data);
        return;
      }
      p = p.left;
    }
  }
}

二叉搜索树删除操作

针对要删除节点的子节点个数的不同，需要分三种情况来处理。

第一种情况是，如果要删除的节点没有子节点，只需要直接将父节点中，指向要删除节点的指针置为 null。

第二种情况是，如果要删除的节点只有一个子节点（只有左子节点或者右子节点），只需要更新父节点中，指向要删除节点的指针，让它指向要删除节点的子节点就可以了。

第三种情况是，如果要删除的节点有两个子节点，这就比较复杂了。我们需要找到这个节点的右子树中的最小节点，把它替换到要删除的节点上。然后再删除掉这个最小节点，因为最小节点肯定没有左子节点（如果有左子结点，那就不是最小节点了），可以应用上面两条规则来删除这个最小节点。

代码实现：

public void delete(int data) {
  Node p = tree; // p指向要删除的节点，初始化指向根节点
  Node pp = null; // pp记录的是p的父节点
  while (p != null && p.data != data) {
    pp = p;
    if (data > p.data) p = p.right;
    else p = p.left;
  }
  if (p == null) return; // 没有找到

  // 要删除的节点有两个子节点
  if (p.left != null && p.right != null) { // 查找右子树中最小节点
    Node minP = p.right;
    Node minPP = p; // minPP表示minP的父节点
    while (minP.left != null) {
      minPP = minP;
      minP = minP.left;
    }
    p.data = minP.data; // 将minP的数据替换到p中
    p = minP; // 下面就变成了删除minP了
    pp = minPP;
  }

  // 删除节点是叶子节点或者仅有一个子节点
  Node child; // p的子节点
  if (p.left != null) child = p.left;
  else if (p.right != null) child = p.right;
  else child = null;

  if (pp == null) tree = child; // 删除的是根节点
  else if (pp.left == p) pp.left = child;
  else pp.right = child;
}

二搜索树时间复杂度分析

平衡二叉查找树的高度接近 logn，插入、删除、查找操作的时间复杂度也比较稳定，时间复杂度是 O(logn)。
最坏情况下，二叉查找树，根节点的左右子树极度不平衡，已经退化成了链表，查找、插入、删除操作的时间复杂度是 O(n)。

LeetCode实战

94. 二叉树的中序遍历

给定一个二叉树，返回它的中序遍历。

示例:

输入: [1,null,2,3]
   1
         2
    /
   3
输出: [1,3,2]

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
 
// 1. 递归 O(n)
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        inorder(root, res);
        return res;
    }

    public void inorder(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        inorder(root.left, res);
        res.add(root.val);
        inorder(root.right, res);
    }
}

// 2. 栈 O(n)
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        Deque<TreeNode> stk = new LinkedList<TreeNode>();
        while (root != null || !stk.isEmpty()) {
            while (root != null) {
                stk.push(root);
                root = root.left;
            }
            root = stk.pop();
            res.add(root.val);
            root = root.right;
        }
        return res;
    }
}

// 3. 莫里斯遍历
/*
Morris 遍历算法是另一种遍历二叉树的方法，它能将非递归的中序遍历空间复杂度降为 O(1)。

Morris 遍历算法整体步骤如下（假设当前遍历到的节点为 x）：

1. 如果 x 无左孩子，先将 x 的值加入答案数组，再访问 x 的右孩子，即 x = x.right。
2. 如果 x 有左孩子，则找到 x 左子树上最右的节点（即左子树中序遍历的最后一个节点，x 在中序遍历中的前驱节点），我们记为 predecessor。根据 predecessor 的右孩子是否为空，进行如下操作。
    2.1 如果 predecessor 的右孩子为空，则将其右孩子指向 x，然后访问 x 的左孩子，即 x = x.left。
    2.2 如果 predecessor 的右孩子不为空，则此时其右孩子指向 x，说明我们已经遍历完 x 的左子树，我们将 predecessor 的右孩子置空，将 x 的值加入答案数组，然后访问 x 的右孩子，即 x = x.right。
3. 重复上述操作，直至访问完整棵树。

时间复杂度：O(n)，其中 nn 为二叉搜索树的节点个数。Morris 遍历中每个节点会被访问两次，因此总时间复杂度为 O(2n)=O(n)
*/
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        TreeNode predecessor = null;

        while (root != null) {
            if (root.left != null) {
                // predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止
                predecessor = root.left;
                while (predecessor.right != null && predecessor.right != root) {
                    predecessor = predecessor.right;
                }
                
                // 让 predecessor 的右指针指向 root，继续遍历左子树
                if (predecessor.right == null) {
                    predecessor.right = root;
                    root = root.left;
                }
                // 说明左子树已经访问完了，我们需要断开链接
                else {
                    res.add(root.val);
                    predecessor.right = null;
                    root = root.right;
                }
            }
            // 如果没有左孩子，则直接访问右孩子
            else {
                res.add(root.val);
                root = root.right;
            }
        }
        return res;
    }
}

144. 二叉树的前序遍历

给定一个二叉树，返回它的前序遍历。

示例:

输入: [1,null,2,3]  
   1
         2
    /
   3 

输出: [1,2,3]

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

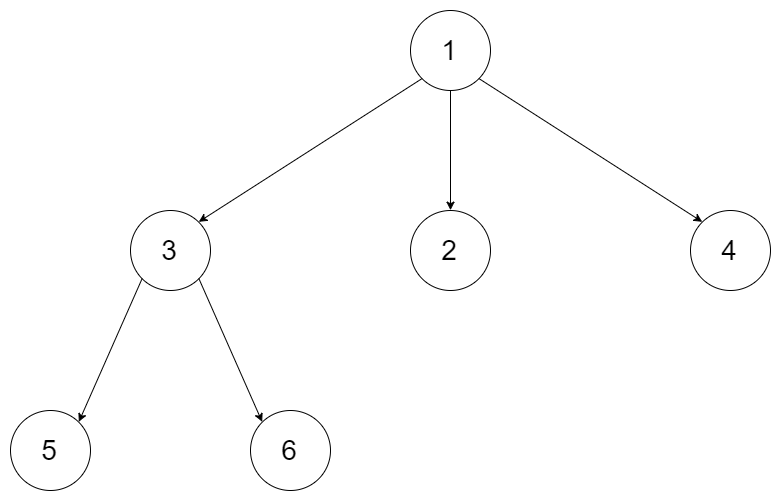
590. N叉树的后序遍历

给定一个 N 叉树，返回其节点值的后序遍历。

例如，给定一个3叉树:

返回其后序遍历: [5,6,3,2,4,1].

说明: 递归法很简单，你可以使用迭代法完成此题吗?

589. N叉树的前序遍历

给定一个 N 叉树，返回其节点值的前序遍历。

例如，给定一个3叉树:

返回其前序遍历: [1,3,5,6,2,4]。

说明: 递归法很简单，你可以使用迭代法完成此题吗?

429. N叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。

例如，给定一个 3叉树 :

返回其层序遍历:

[
     [1],
     [3,2,4],
     [5,6]
]

说明:

树的深度不会超过 1000。
树的节点总数不会超过 5000。

参考文献：

算法训练营-覃超
数据结构与算法之美-王争
算法图解
维基百科
LeetCode

数据结构与算法（Ⅳ）：树、二叉树、二叉搜索树

原文：https://www.cnblogs.com/haif/p/13676524.html

hmoban主题是根据ripro二开的主题，极致后台体验，无插件，集成会员系统
自学咖网 » 数据结构与算法（Ⅳ）：树、二叉树、二叉搜索树

wen 普通

分享到：

树（Tree）

二叉树（Binary Tree）

二叉树遍历

二叉搜索树（Binary Search Tree）

二叉搜索树查找操作

二叉搜索树插入操作

二叉搜索树删除操作

二搜索树时间复杂度分析

LeetCode实战

94. 二叉树的中序遍历

144. 二叉树的前序遍历

590. N叉树的后序遍历

589. N叉树的前序遍历

429. N叉树的层序遍历

wen 普通

相关推荐