红黑树中添加元素
听一些同事出去面试被问到 hashMap 的 红黑色的添加元素的过程。表示我没有被到过,估计是面试不多吧。
其实呢 有点不好理解,也不好记
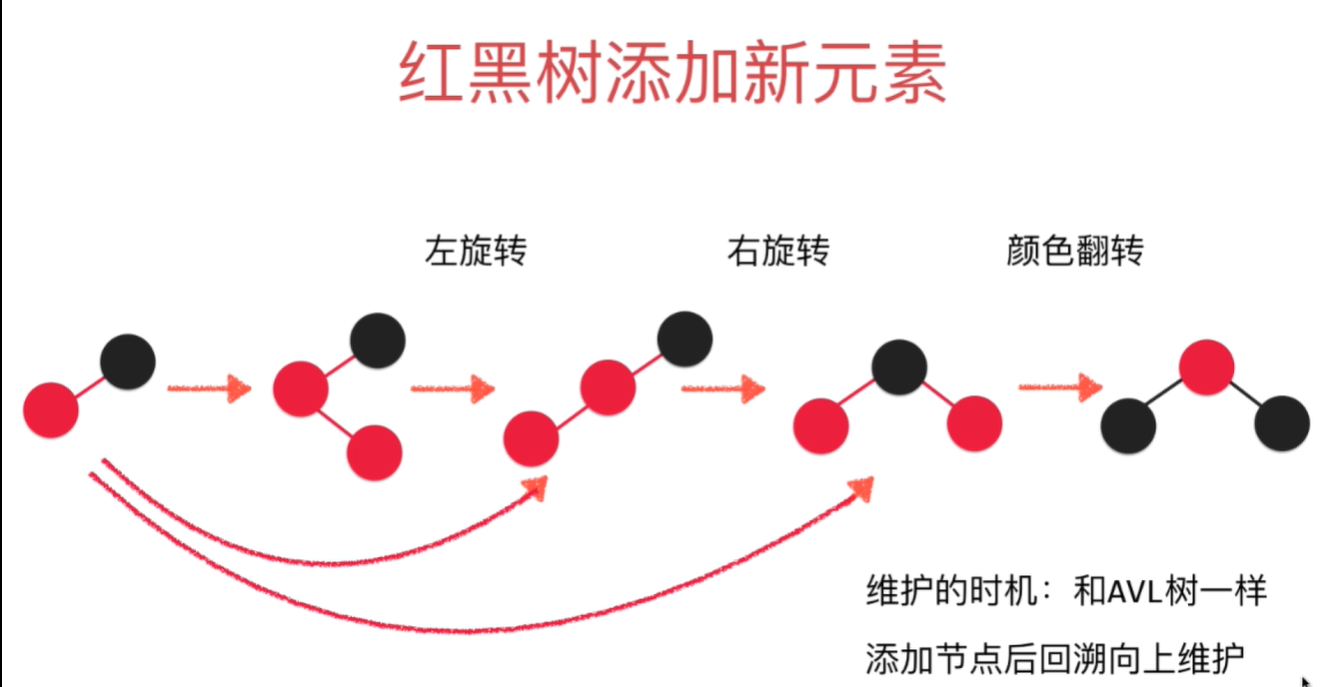
上图总结得比较好了。也比较好记 。请记住
红黑树 等价于 2-3树 。 即 黑色节点的左孩子是红色的,可以把他们看成 2-3 树中的 一个 包含2个元素的 一个节点
正常的红黑树, 红色节点 总是在 父节点的 左侧的(不是就得进行变化) ,即左倾
红黑树的 根节点 肯定是 黑色的 (即 变色旋转到了最后 如果 根节点不是 黑色,那么就变成黑色 )
红黑树是 符合 二分搜索树的,即 父亲节点大于左孩子,小于右孩子
1. 新添加的节点默认 是 红色的节点(如果 是一个节点,即是 根节点,那么就变成 黑色)
2. 当只有一个 黑色根节点添加一个比它大的红色节点的时候,即在根节点的右侧, 此时不符合红黑树规则,
那么它就会进行左旋 : 原来的根节点变成 新加入的节点的左孩子,并变成 红色, 而 新的节点变成了根节点,变成了红色
接着添加节点的变化情况就如同上图的变化情况了。 总结得很清晰好记了。
代码例子
import java.util.ArrayList;
public class RBTree<K extends Comparable<K>, V> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node{
public K key;
public V value;
public Node left, right;
public boolean color;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
color = RED;
}
}
private Node root;
private int size;
public RBTree(){
root = null;
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// 判断节点node的颜色
private boolean isRed(Node node){
if(node == null)
return BLACK;
return node.color;
}
// node x
// / 左旋转 /
// T1 x ---------> node T3
// / /
// T2 T3 T1 T2
private Node leftRotate(Node node){
Node x = node.right;
// 左旋转
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
// node x
// / 右旋转 /
// x T2 -------> y node
// / /
// y T1 T1 T2
private Node rightRotate(Node node){
Node x = node.left;
// 右旋转
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
// 颜色翻转
private void flipColors(Node node){
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
// 向红黑树中添加新的元素(key, value)
public void add(K key, V value){
root = add(root, key, value);
root.color = BLACK; // 最终根节点为黑色节点
}
// 向以node为根的红黑树中插入元素(key, value),递归算法
// 返回插入新节点后红黑树的根
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value); // 默认插入红色节点
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
//左孩子节点不是黑色,右孩子节点是 红色, 左旋
if (isRed(node.right) && !isRed(node.left))
node = leftRotate(node);
// 左孩子节点是红色节点,左孩子的左孩子节点是 红色, 右旋
if (isRed(node.left) && isRed(node.left.left))
node = rightRotate(node);
// 左孩子节点是红色节点, 右孩子节点也是 红色 节点 , 颜色翻转
if (isRed(node.left) && isRed(node.right))
flipColors(node);
return node;
}
// 返回以node为根节点的二分搜索树中,key所在的节点
private Node getNode(Node node, K key){
if(node == null)
return null;
if(key.equals(node.key))
return node;
else if(key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
public boolean contains(K key){
return getNode(root, key) != null;
}
public V get(K key){
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue){
Node node = getNode(root, key);
if(node == null)
throw new IllegalArgumentException(key + " doesn"t exist!");
node.value = newValue;
}
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 从二分搜索树中删除键为key的节点
public V remove(K key){
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key){
if( node == null )
return null;
if( key.compareTo(node.key) < 0 ){
node.left = remove(node.left , key);
return node;
}
else if(key.compareTo(node.key) > 0 ){
node.right = remove(node.right, key);
return node;
}
else{ // key.compareTo(node.key) == 0
// 待删除节点左子树为空的情况
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// 待删除节点右子树为空的情况
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
public static void main(String[] args){
System.out.println("Pride and Prejudice");
ArrayList<String> words = new ArrayList<>();
if(FileOperation.readFile("pride-and-prejudice.txt", words)) {
System.out.println("Total words: " + words.size());
RBTree<String, Integer> map = new RBTree<>();
for (String word : words) {
if (map.contains(word))
map.set(word, map.get(word) + 1);
else
map.add(word, 1);
}
System.out.println("Total different words: " + map.getSize());
System.out.println("Frequency of PRIDE: " + map.get("pride"));
System.out.println("Frequency of PREJUDICE: " + map.get("prejudice"));
}
System.out.println();
}
}


