[编程题] lk [152. 乘积最大子数组-二维动态规划]

[编程题] lk 152. 乘积最大子数组-二维动态规划

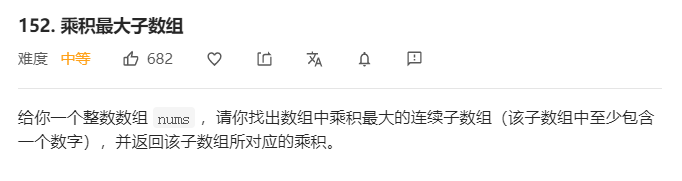
题目

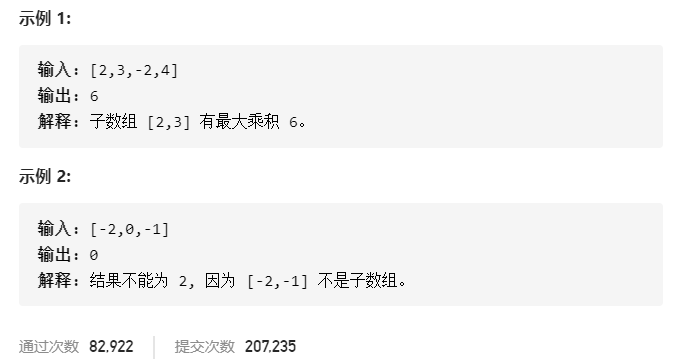
输入输出

方法1：使用一个二维的dp来表示当前节点的最大值和最小值情况

思想：

? 每个dp[i]位置用两个维度表示值信息，dp[i][0]表示目前的最大值情况,dp[i][1]表示目前的最小值情况如负数
? ① 我们在遍历数组的时候，如果碰到nums[i]是负数，那么我们拿出上一个状态dp[i]的最小值即dp[i][1]得出的结果一定是正,这样子的情况最大；

? ② 我们在遍历数组的时候，如果碰到nums[i]是正数，那么我们拿出上一个状态dp[i]的最大值即dp[i][0]得出的结果一定是正,这样子的情况最大、

总结来说，我们算当前的dp【i】【0】即是算最大值，即求

max(dp[i-1][0]*nums[i],dp[i-1][1]*nums[i], nums[i])

总结来说，我们算当前的dp【i】【1】即是算最小值，即求

mix(dp[i-1][0]*nums[i],dp[i-1][1]*nums[i], nums[i])

方法：动态规划（二维dp）

class Solution {
    //方法1：动态规划(使用二维数组表示dp状态)
    public int maxProduct(int[] nums) {
        int[][] dp = new int[nums.length][2];  //其中的0维度表示该数为止的max值，1维度表示该数为止的最小值
        dp[0][0] = nums[0]; //默认dp[0]最大值
        dp[0][1] = nums[0]; //默认dp[0]最小值
        int max = dp[0][0]; //记录最大值
        for(int i=1;i<nums.length;i++){
            //本质是max(dp[i-1][0]*nums[i],dp[i-1][1]*nums[i], nums[i]),Java API只能接收俩参数
            dp[i][0] = Math.max(dp[i-1][0]*nums[i], Math.max(dp[i-1][1]*nums[i], nums[i])); //最大值
            dp[i][1] = Math.min(dp[i-1][0]*nums[i], Math.min(dp[i-1][1]*nums[i], nums[i])); //最小值
            max = Math.max(max, dp[i][0]);
        }
        return max;
    }
}

方法2：我们用两个dp[]一维数组来表示当前状态的最大值和最小值数组

思想：

? 本质和上述没区别，只是我们分了两个dp[]一维数组来分别表达dp[i]的max和min,在计算的时候也是类似上边的情况得到最大最小值。

Java代码

//方法2：我们用两个dp[]一维数组来表示当前状态的最大值和最小值数组
    public int maxProduct(int[] nums) {
        int[] dpMax = new int[nums.length];  //表示当前节点的最大值
        int[] dpMin = new int[nums.length];  //表示当前节点的最小值

        dpMax[0] = nums[0]; //最大值的首节点
        dpMin[0] = nums[0]; //最小值的首节点

        int max = nums[0]; //默认的最大值
        for(int i=1;i<nums.length;i++){
            dpMax[i] = Math.max(dpMax[i-1]*nums[i],Math.max(dpMin[i-1]*nums[i],nums[i]));
            dpMin[i] = Math.min(dpMax[i-1]*nums[i],Math.min(dpMin[i-1]*nums[i],nums[i]));
            max = max>dpMax[i]?max:dpMax[i];
        }
        return max;
    }

输出：

[编程题] lk [152. 乘积最大子数组-二维动态规划]

原文地址：https://www.cnblogs.com/jiyongjia/p/13405963.html