数据结构实验（四）

树和二叉树

1. 二叉树的封装与遍历

   • “BinTree.hpp”

     // Test6-1：二叉树的封装与遍历
     
     #pragma once
     #include <iostream>
     using namespace std;
     
     static char screen[40][80];		//屏幕打印专用的缓冲区
     
     template <typename Element>
     struct BinTree {
     	Element data;				//结点数据	
     	BinTree* lchild;			//左孩子
     	BinTree* rchild;			//右孩子
     
     	BinTree(Element data)		//构造函数
     	{
     		this->data = data;
     		lchild = NULL;
     		rchild = NULL;
     	}
     
     	~BinTree()					//析构函数，递归释放子结点
     	{
     		if (lchild)
     			delete lchild;
     		if (rchild)
     			delete rchild;
     	}
     
     	static BinTree* create(const char* str, int& index)
     	{
     		//实现由先序遍历字符串 创建二叉树
     		char ch = str[index++];
     		if (ch == "#")
     			return NULL;
     		BinTree* node = new BinTree(ch);
     		node->lchild = create(str, index);
     		node->rchild = create(str, index);
     		return node;
     	}
     
     	int deep()
     	{
     		//递归求数的深度
     		int ldeep = (lchild == NULL) ? 0 : lchild->deep();
     		int rdeep = (rchild == NULL) ? 0 : rchild->deep();
     		return 1 + (ldeep > rdeep ? ldeep : rdeep);
     	}
     
     	BinTree* create()
     	{
     		//输入含叶子结点空指针标记的方式创建二叉树
     		char ch;
     		scanf("%c", &ch);
     		if (ch == "#")
     			return NULL;
     		BinTree* node = new BinTree(ch);
     		node->lchild = create();
     		node->rchild = create();
     		return node;
     	}
     
     	void output()
     	{
     		//输出整个二叉树
     		memset(screen, " ", sizeof(screen));	//不打印的地方用空格占位
     		draw(0, 0, NULL);						//从(0,0)坐标和根节点开始，绘制树到screen缓冲区
     		int height = deep() * 2;				//打印高度等于树深度的2倍，因为元素值要间隔一行
     		for (int i = 0; i < height; i++)
     		{
     			screen[i][40] = "";
     			printf("%s
     ", screen[i]);
     		}
     	}
     
     	int draw(int startx, int y, BinTree* parent)
     	{
     		//利用中序遍历在screen缓冲区中绘制二叉树图形
     		//startx表示当前树最左端的起始x坐标
     		//endx表示当前子树最右端的x坐标
     		int endx = startx;
     		if (lchild)								//先左子树
     			endx = lchild->draw(startx, y + 2, this) + 1;
     		int centerx = endx;						//左子树结束的x坐标，就是根结点的x坐标
     		screen[y][endx] = data;					//根结点的内容
     		if (rchild)								//后右子树
     		{
     			endx++;
     			endx = rchild->draw(endx, y + 2, this) + 1;
     		}
     
     
     		if (parent)
     		{
     			//如果有父结点，下面的处理负责把自己的根结点打印连接线到父结点
     			if (parent->lchild == this)
     			{
     				for (int x = centerx; x < endx; x++)
     					screen[y - 1][x] = "-";
     				screen[y - 1][centerx] = "/";
     			}
     			else
     			{
     				for (int x = startx; x <= centerx; x++)
     					screen[y - 1][x] = "-";
     				screen[y - 1][centerx] = "\";
     			}
     		}	
     		return endx;
     	}
     
     	void preOrder()
     	{
     		//实现先序遍历
     		printf("%c ", data);
     		if (lchild)
     			lchild->preOrder();
     		if (rchild)
     			rchild->preOrder();
     	}
     
     	void middleOrder()
     	{
     		//实现中序遍历
     		if (lchild)
     			lchild->middleOrder();
     		printf("%c ", data);
     		if (rchild)
     			rchild->middleOrder();
     	}
     
     	void postOrder()
     	{
     		//实现后序遍历
     		if (lchild)
     			lchild->postOrder();
     		if (rchild)
     			rchild->postOrder();
     		printf("%c ", data);
     	}
     
     	static BinTree* rebuildByPreIn(const char* PreOrder, const char* InOrder, int Len)
     	{
     		//由先序和中序重构二叉树
     		//如果先序遍历为空，则返回空值
     		if (Len == 0)
     			return NULL;
     		//取PerOder中的第一个元素作为头结点r
     		char r = PreOrder[0] - 32;		//将小写字母转为大写字母
     		BinTree* R = new BinTree(r);
     		//在InOder中查找r出现的位置pos
     		int pos = 0;
     		while (pos < Len)
     		{
     			if (InOrder[pos] - 32 == r)
     				break;
     			pos++;
     		}
     		//重构左子树
     		R->lchild = rebuildByPreIn(PreOrder + 1, InOrder, pos);
     		pos++;
     		//重构右子树
     		R->rchild = rebuildByPreIn(PreOrder + pos, InOrder + pos, Len - pos);
     		return R;
     	}
     };
     

   • “BinTree.cpp”

     #include <iostream>
     #include "./BinTree.hpp"
     
     using namespace std;
     
     int main()
     {
     	//二叉树创建、遍历、重构和输出测试用例
     	typedef BinTree<char> BinTree;
     	BinTree* tree;
     	int index = 0;
     	tree = BinTree::create("AB##CDF###E##", index);
     	tree->output();
     	cout << "先序遍历顺序为：";
     	tree->preOrder();
     	cout << "
     中序遍历顺序为：";
     	tree->middleOrder();
     	cout << "
     后序遍历顺序为：";
     	tree->postOrder();
     	delete tree;
     	cout << endl;
     	cout << endl;
     	//已知先序和中序遍历重构二叉树
     	tree = BinTree::rebuildByPreIn("abdgcefh", "dgbaechf", 8);
     	tree->output();
     	delete tree;
     
     	return 0;
     }
     

   • 运行截图：

     

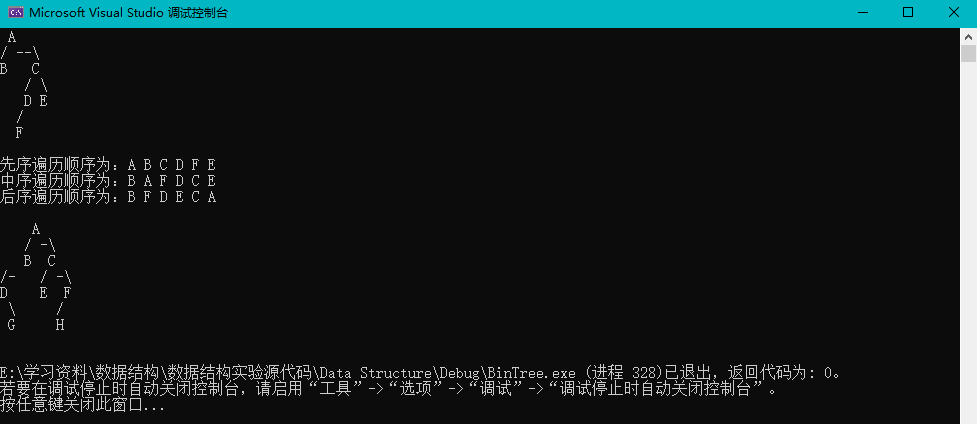
2. Huffman树的封装与编解码

   • “HuffmanTree.hpp”

     // Test6-2：Huffman树的封装与编解码
     
     #include <iostream>
     #include <string.h>
     using namespace std;
     #include "..//BinTree/BinTree.hpp"
     
     // Huffman树的结点的封装
     struct HuffmanNode
     {
     	char data;				// 字符
     	float weight;			// 权重
     	char code[10];			// 编码
     	int depth;				// 深度
     	int lchild, rchild;		// 左右子结点的下标，为0表示该结点为叶子结点
     	int parent;				// 父结点的下标，为0表示当前结点是根结点
     
     	HuffmanNode()
     	{
     		data = " ";
     		weight = 999;
     		lchild = rchild = parent = 0;
     		code[0] = "";
     	}
     
     	~HuffmanNode()
     	{
     		if (code)
     			delete code;
     	}
     
     	void output()
     	{
     		// 结点的输出函数
     		printf("%.f	%d	%d	%d	", weight, lchild, rchild, parent);
     		if (code)
     			printf("%c	%s", data, code);
     		cout << endl;
     	}
     
     	bool isLeaf()
     	{
     		// 判断当前结点是否为叶子结点
     		if (lchild == rchild == 0)
     			return true;
     		else
     			return false;
     	}
     };
     
     // Huffman树的封装
     struct HuffmanTree
     {	
     	HuffmanNode *nodes;		// TODO：用顺序表封装可扩容的结点数组
     	int n;					// 表示编码的数量
     	char table[128];		//ASCII索引表
     
     	HuffmanTree(int n)
     	{
     		this->n = n;
     		nodes = new HuffmanNode[2 * n];
     	}
     
     	~HuffmanTree()
     	{
     		delete[] nodes;
     	}
     
     	void create(const char* charset, int weight[])		// 根据传入的data和weight来创建Huffman树
     	{
     		// 记录字符ASCII码到编码表下标的映射关系
     		for (int i = 0; i < n; i++)
     			table[charset[i]] = i + 1;
     		// 通过填表完成建树，注意nodes下标从1开始
     		// 填叶子结点
     		for (int i = 1; i <= n; i++)
     		{
     			nodes[i].data = charset[i - 1];
     			nodes[i].weight = weight[i - 1];
     		}
     		// 填非叶子结点
     		for (int i = n + 1; i < 2 * n ; i++)
     		{
     			int idx1 = 2 * n - 1, idx2 = 2 * n - 1;		// 给最小和次小的结点下标赋初值	
     			findMinial12(i, idx1, idx2);	// 返回在i结点前权值最小的两个结点的下标
     			nodes[i].weight = nodes[idx1].weight + nodes[idx2].weight;
     			// 找孩子结点
     			nodes[i].lchild = idx1;
     			nodes[i].rchild = idx2;
     			// 找父亲结点
     			nodes[idx1].parent = i;
     			nodes[idx2].parent = i;
     		}
     
     		// 通过遍历Huffman树来填写编码
     		char code[10] = { 0 };
     		fillCode(2 * n - 1, code, 0);
     	}
     
     	void findMinial12(int i, int& idx1, int& idx2)	//传入引用类型的下标，将函数实参与形参内存绑定，，所以无需返回值
     	{
     		// 在nodes的第i个结点之前，找到权值最小的两个结点的下标
     		for (int k = 1; k < i; k++)
     		{
     			if (nodes[k].parent != 0) continue;		// 父结点非零，即已经参与findMinial12()的结点不进行比较
     			if (nodes[k].weight > nodes[idx2].weight) continue;		// 权重比次小大的无需更新最小次小下标
     			if (nodes[k].weight < nodes[idx1].weight)
     			{
     				// 比最小还小，更新最小和次小
     				idx2 = idx1;
     				idx1 = k;
     			}
     			else
     				// 比次小小比最小大，更新次小
     				idx2 = k;
     		}
     	}
     
     	void fillCode(int node, char code[], int depth)
     	{
     		if (node <= n)
     		{
     			// 遍历到叶子结点，获得编码
     			code[depth] = "";
     			nodes[node].depth = depth;
     			strcpy_s(nodes[node].code, code);
     			return;
     		}
     		else if (node < 2 * n - 1)
     		{
     			// 遍历到除根结点外的非叶子结点，获得编码
     			code[depth] = "";
     			strcpy_s(nodes[node].code, code);
     		}
     		// 产生左分支的编码
     		code[depth] = "0";
     		// 递归遍历左子树
     		fillCode(nodes[node].lchild, code, depth + 1);
     
     		// 产生右分支的编码
     		code[depth] = "1";
     		// 递归遍历右子树
     		fillCode(nodes[node].rchild, code, depth + 1);
     	}
     
     	void output()
     	{
     		printf("序号	权重	左结点	右结点	父结点	字符	编码
     ");
     		for (int i = 1; i < 2 * n; i++)
     		{
     			printf("%d	", i);
     			nodes[i].output();
     		}
     		cout << endl;
     	}
     
     	void enCode(const char* plain, char * buffer)	// 利用Huffman树进行编码
     	{
     		while (*plain)
     		{
     			char ch = *plain;						// 取出带编码的字符
     			char* str = nodes[table[ch]].code;
     			strcat_s(buffer, sizeof(buffer) + strlen(str), str); // 字符串拼接到buffer中
     			plain++;								// 移动到下一个字符	
     		}
     	}
     
     	void deCode()					// 利用Huffman树进行解码
     	{
     		// TODO：解码的实现
     	}
     };
     

   • “HuffmanTree.cpp”

     #include <iostream>
     #include "./HuffmanTree.hpp"
     
     using namespace std;
     
     int main()
     {
     	//Huffman树创建、编码、解码和输出用例
     	HuffmanTree tree(4);
     	int weight[] = { 7,5,2,4 };
     	tree.create("abcd", weight);
     	tree.output();
     	char buffer[10] = { 0 };
     	tree.enCode("bad", buffer);
     	cout << "bad的编码为：" << buffer << endl;
     	return 0;
     }
     

   • 运行截图：
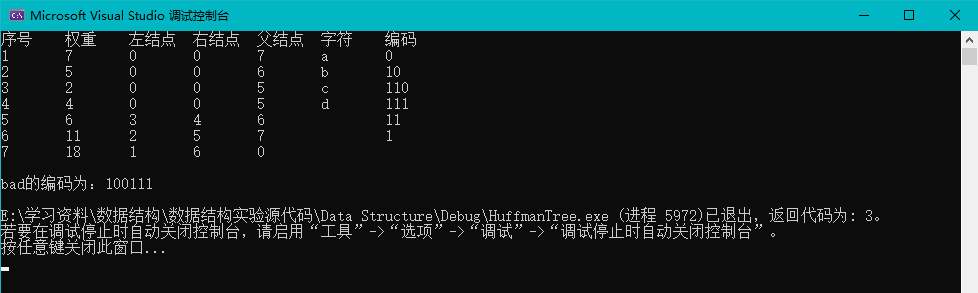