python中如何遍历树

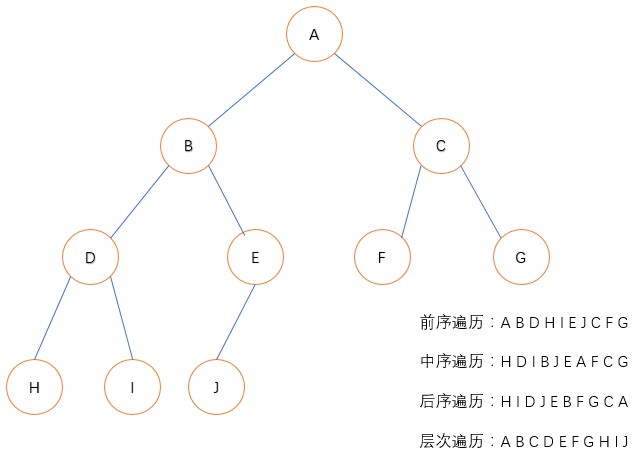
各种遍历顺序如下图所示：

树的最大深度 

# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution(object):
    def maxdepth(self, root):
        if root is None:
            return 0
        return max(self.maxdepth(root.left), self.maxdepth(root.right))+1

深度优先

深度优先遍历有三种方式：前序遍历、中序遍历和后序遍历

所说的前序、中序、后序，是指根节点的先后顺序。

前序遍历：根节点 -> 左子树 -> 右子树

# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution(object):
    def preorder(self, root):
        if root is None:
            return ''
        print root.val
        if root.lef:
            self.preorder(root.left)
        if root.right:
            self.preorder(root.right)

中序遍历：左子树 -> 根节点 -> 右子树

# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution(object):
    def midorder(self, root):
        if root is None:
            return ''
        if root.lef:
            self.midorder(root.left)
        print root.val
        if root.right:
            self.midorder(root.right)

后序遍历：左子树 -> 右子树 -> 根节点

# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution(object):
    def endorder(self, root):
        if root is None:
            return ''
        if root.lef:
            self.endorder(root.left)
        if root.right:
            self.endorder(root.right)
        print root.val

广度优先

广度优先遍历，即层次遍历，优先遍历兄弟节点

层次遍历：根节点 -> 左节点 -> 右节点

# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution(object):
　　def graorder(self, root):
　　　　if root is None:
　　　　　　return ''
　　　　queue = [root]
　　　　while queue:
　　　　　　res = []
　　　　　　for item in queue:
　　　　　　　　print item.val,
　　　　　　　　if item.left:
　　　　　　　　　　res.append(item.left)
　　　　　　　　if item.right:
　　　　　　　　　　res.apppend(item.right)
　　　　　　queue = res

比较两棵树是否相同

# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution(object):
    def issame(self, root1, root2):
        if root1 is None and root2 is None:
            return True
        elif root1 and root2:
            return root1.val==root2.val and issame(root1.left, root2.left) and issame(root1.right, root2.right)
        else:
            return False

众多python教程，尽在云海天教程网，欢迎在线学习！

来源：PY学习网：原文地址：https://www.py.cn/article.html