Python数学建模三剑客之Numpy

三剑客之Numpy
numpy是一个开源的python科学计算库,包含了很多实用的数学函数,涵盖线性代数、傅里叶变换和随机数生成等功能。最初的numpy其实是scipy的一部分,后来才从scipy中分离出来。
numpy不是python的标准库,需要单独安装。假定你的运行环境已经安装了python包管理工具pip,numpy的安装就非常简单:
pip install numpy
一、数组对象
ndarray是多维数组对象,也是numpy最核心的对象。在numpy中,数组的维度(dimensions)叫做轴(axes),轴的个数叫做秩(rank)。通常,一个numpy数组的所有元素都是同一种类型的数据,而这些数据的存储和数组的形式无关。
下面的例子,创建了一个三维的数组(在导入numpy时,一般都简写成np)。
import numpy as np a = np.array([[1,2,3],[4,5,6],[7,8,9]])
1、数据类型
numpy支持的数据类型主要有布尔型(bool)、整型(integrate)、浮点型(float)和复数型(complex),每一种数据类型根据占用内存的字节数又分为多个不同的子类型。常见的数据类型见下表。
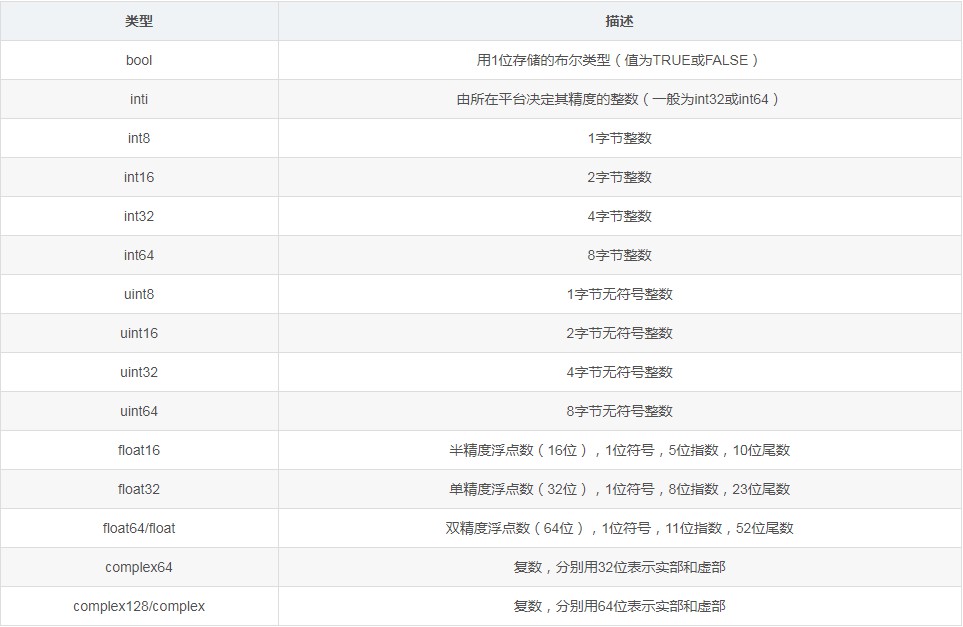
2、创建数组
通常,我们用np.array()创建数组。如果仅仅是创建一维数组,也可以使用np.arange()或者np.linspace()的方法。np.zeros()、np.ones()、np.eye()则可以构造特殊的数据。np.random.randint()和np.random.random()则可以构造随机数数组。
>>> np.array([[1,2,3],[4,5,6]]) # 默认元素类型为int32 array([[1, 2, 3], [4, 5, 6]]) >>> np.array([[1,2,3],[4,5,6]], dtype=np.int8) # 指定元素类型为int8 array([[1, 2, 3], [4, 5, 6]], dtype=int8) >>> np.arange(5) # 默认元素类型为int32 array([0, 1, 2, 3, 4]) >>> np.arange(3,8, dtype=np.int8) # 指定元素类型为int8 array([3, 4, 5, 6, 7], dtype=int8) >>> np.arange(12).reshape(3,4) # 改变shape array([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]]) >>> np.linspace(1,2,5) # 从1到2生成5个浮点数 array([ 1. , 1.25, 1.5 , 1.75, 2. ]) >>> np.zeros((2,3)) # 全0数组 array([[ 0., 0., 0.], [ 0., 0., 0.]]) >>> np.ones((2,3)) # 全1数组 array([[ 1., 1., 1.], [ 1., 1., 1.]]) >>> np.eye(3) # 主对角线元素为1其他元素为0 array([[ 1., 0., 0.], [ 0., 1., 0.], [ 0., 0., 1.]]) >>> np.random.random((2,3)) # 生成[0,1)之间的随机浮点数 array([[ 0.84731148, 0.8222318 , 0.85799278], [ 0.59371558, 0.92330741, 0.04518351]]) >>> np.random.randint(0,10,(3,2)) # 生成[0,10)之间的随机整数 array([[2, 4], [8, 3], [8, 5]])
3、构造复杂数组
很多时候,我们需要从简单的数据结构,构造出复杂的数组。例如,用一维的数据生成二维格点。
(1)重复数组:tile
>>> a = np.arange(5) >>> a array([0, 1, 2, 3, 4]) >>> np.tile(a, 2) array([0, 1, 2, 3, 4, 0, 1, 2, 3, 4]) >>> np.tile(a, (3,2)) array([[0, 1, 2, 3, 4, 0, 1, 2, 3, 4], [0, 1, 2, 3, 4, 0, 1, 2, 3, 4], [0, 1, 2, 3, 4, 0, 1, 2, 3, 4]])
(2)重复元素:repeat
>>> a = np.arange(5) >>> a array([0, 1, 2, 3, 4]) >>> a.repeat(2) array([0, 0, 1, 1, 2, 2, 3, 3, 4, 4])
(3)一维数组网格化:meshgrid
>>> a = np.arange(5) >>> b = np.arange(5,10) >>> np.meshgrid(a,b) [array([[0, 1, 2, 3, 4], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4], [0, 1, 2, 3, 4]]), array([[5, 5, 5, 5, 5], [6, 6, 6, 6, 6], [7, 7, 7, 7, 7], [8, 8, 8, 8, 8], [9, 9, 9, 9, 9]])] >>>
(4)指定范围和分割方式的网格化:mgrid
>>> np.mgrid[0:1:2j, 1:2:3j] array([[[ 0. , 0. , 0. ], [ 1. , 1. , 1. ]], [[ 1. , 1.5, 2. ], [ 1. , 1.5, 2. ]]]) >>> np.mgrid[0:1:0.3, 1:2:0.4] array([[[ 0. , 0. , 0. ], [ 0.3, 0.3, 0.3], [ 0.6, 0.6, 0.6], [ 0.9, 0.9, 0.9]], [[ 1. , 1.4, 1.8], [ 1. , 1.4, 1.8], [ 1. , 1.4, 1.8], [ 1. , 1.4, 1.8]]])
上面的例子中用到了虚数。构造虚数的方法如下:
>>> complex(2,5) (2+5j)
4、数组的属性
numpy的数组对象除了一些常规的属性外,也有几个类似转置、扁平迭代器等看起来更像是方法的属性。扁平迭代器也许是遍历多维数组的一个简明方法,下面的代码给出了一个例子。
>>> a = np.array([[1,2,3],[4,5,6]])
>>> a.dtype # 数组元素的数据类型
dtype('int32')
>>> a.dtype.itemsize # 数组元素占据的内存字节数
4
>>> a.itemsize # 数组元素占据的内存字节数
4
>>> a.shape # 数组的维度
(2, 3)
>>> a.size # 数组元素个数
6
>>> a.T # 数组行变列,类似于transpose()
array([[1, 4],
[2, 5],
[3, 6]])
>>> a.flat # 返回一个扁平迭代器,用于遍历多维数组
<numpy.flatiter object at 0x037188F0>
>>> for item in a.flat:
print item
5、改变数组维度
numpy数组的存储顺序和数组的维度是不相干的,因此改变数组的维度是非常便捷的操作,除resize()外,这一类操作不会改变所操作的数组本身的存储顺序。
>>> a = np.array([[1,2,3],[4,5,6]]) >>> a.shape # 查看数组维度 (2, 3) >>> a.reshape(3,2) # 返回3行2列的数组 array([[1, 2], [3, 4], [5, 6]]) >>> a.ravel() # 返回一维数组 array([1, 2, 3, 4, 5, 6]) >>> a.transpose() # 行变列(类似于矩阵转置) array([[1, 4], [2, 5], [3, 6]]) >>> a.resize((3,2)) # 类似于reshape,但会改变所操作的数组 >>> a array([[1, 2], [3, 4], [5, 6]])
6、索引和切片
对于一维数组的索引和切片,numpy和python的list一样,甚至更灵活。
a = np.arange(9) >>> a[-1] # 最后一个元素 8 >>> a[2:5] # 返回第2到第5个元素 array([2, 3, 4]) >>> a[:7:3] # 返回第0到第7个元素,步长为3 array([0, 3, 6]) >>> a[::-1] # 返回逆序的数组 array([8, 7, 6, 5, 4, 3, 2, 1, 0])
假设有一栋2层楼,每层楼内的房间都是3排4列,那我们可以用一个三维数组来保存每个房间的居住人数(当然,也可以是房间面积等其他数值信息)。
>>> a = np.arange(24).reshape(2,3,4) # 2层3排4列 >>> a array([[[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]], [[12, 13, 14, 15], [16, 17, 18, 19], [20, 21, 22, 23]]]) >>> a[1][2][3] # 虽然可以这样 23 >>> a[1,2,3] # 但这才是规范的用法 23 >>> a[:,0,0] # 所有楼层的第1排第1列 array([ 0, 12]) >>> a[0,:,:] # 1楼的所有房间,等价与a[0]或a[0,...] array([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]]) >>> a[:,:,1:3] # 所有楼层所有排的第2到4列 array([[[ 1, 2], [ 5, 6], [ 9, 10]], [[13, 14], [17, 18], [21, 22]]]) >>> a[1,:,-1] # 2层每一排的最后一个房间 array([15, 19, 23])
7、数组合并
数组合并除了下面介绍的水平合并、垂直合并、深度合并外,还有行合并、列合并,以及concatenate()等方式。假如你比我还懒,那就只了解前三种方法吧,足够用了。
>>> a = np.arange(9).reshape(3,3) >>> b = np.arange(9,18).reshape(3,3) >>> a array([[0, 1, 2], [3, 4, 5], [6, 7, 8]]) >>> b array([[ 9, 10, 11], [12, 13, 14], [15, 16, 17]]) >>> np.hstack((a,b)) # 水平合并 array([[ 0, 1, 2, 9, 10, 11], [ 3, 4, 5, 12, 13, 14], [ 6, 7, 8, 15, 16, 17]]) >>> np.vstack((a,b)) # 垂直合并 array([[ 0, 1, 2], [ 3, 4, 5], [ 6, 7, 8], [ 9, 10, 11], [12, 13, 14], [15, 16, 17]]) >>> np.dstack((a,b)) # 深度合并 array([[[ 0, 9], [ 1, 10], [ 2, 11]], [[ 3, 12], [ 4, 13], [ 5, 14]], [[ 6, 15], [ 7, 16], [ 8, 17]]])
8、数组拆分
拆分是合并的逆过程,概念是一样的,但稍微有一点不同:
>>> a = np.arange(9).reshape(3,3) >>> np.hsplit(a, 3) # 水平拆分,返回list [array([[0], [3], [6]]), array([[1], [4], [7]]), array([[2], [5], [8]])] >>> np.vsplit(a, 3) # 垂直拆分,返回list [array([[0, 1, 2]]), array([[3, 4, 5]]), array([[6, 7, 8]])] >>> a = np.arange(27).reshape(3,3,3) >>> np.dsplit(a, 3) # 深度拆分,返回list [array([[[ 0], [ 3], [ 6]], [[ 9], [12], [15]], [[18], [21], [24]]]), array([[[ 1], [ 4], [ 7]], [[10], [13], [16]], [[19], [22], [25]]]), array([[[ 2], [ 5], [ 8]], [[11], [14], [17]], [[20], [23], [26]]])]
9、数组运算
数组和常数的四则运算,是数组的每一个元素分别和常数运算;数组和数组的四则运算则是两个数组对应元素的运算(两个数组有相同的shape,否则抛出异常)。
>>> a = np.arange(4, dtype=np.float32).reshape(2,2) >>> b = np.arange(4, 8, dtype=np.float32).reshape(2,2) >>> a+2 # 数组和常数可以进行四则运算 array([[ 2., 3.], [ 4., 5.]], dtype=float32) >>> a/b # 数组和数组可以进行四则运算 array([[ 0. , 0.2 ], [ 0.33333334, 0.42857143]], dtype=float32) >>> a == b # 最神奇的是,数组可以判断对应元素是否相等 array([[False, False], [False, False]], dtype=bool) >>> (a == b).all() # 判断数组是否相等 False
特别提示:如果想对数组内符合特定条件的元素做特殊处理,下面的代码也许有用。
>>> a = np.arange(6).reshape((2,3)) >>> a array([[0, 1, 2], [3, 4, 5]]) >>> (a>2)&(a<=4) array([[False, False, False], [ True, True, False]], dtype=bool) >>> a[(a>2)&(a<=4)] array([3, 4]) >>> a[(a>2)&((a<=4))] += 10 >>> a array([[ 0, 1, 2], [13, 14, 5]])
10、数组方法和常用函数
数组对象本身提供了计算算数平均值、求最大最小值等内置方法,numpy也提供了很多实用的函数。为了缩减篇幅,下面的代码仅以一维数组为例,展示了这些方法和函数用法。事实上,大多数情况下这些方法和函数对于多维数组同样有效,只有少数例外,比如compress函数。
>>> a = np.array([3,2,4]) >>> a.sum() # 所有元素的和 9 >>> a.prod() # 所有元素的乘积 24 >>> a.mean() # 所有元素的算数平均值 3.0 >>> a.max() # 所有元素的最大值 4 >>> a.min() # 所有元素的最小值 2 >>> a.clip(3,4) # 小于3的元素替换为3,大于4的元素替换为4 array([3, 3, 4]) >>> a.compress(a>2) # 返回大于2的元素组成的数组 array([3, 4]) >>> a.tolist() # 返回python的list [3, 2, 4] >>> a.var() # 计算方差(元素与均值之差的平方的均值) 0.66666666666666663 >>> a.std() # 计算标准差(方差的算术平方根) 0.81649658092772603 >>> a.ptp() # 返回数组的最大值和最小值之差 2 >>> a.argmin() # 返回最小值在扁平数组中的索引 1 >>> a.argmax() # 返回最大值在扁平数组中的索引 2 >>> np.where(a == 2) # 返回所有值为2的元素的索引 (array([1]),) >>> np.diff(a) # 返回相邻元素的差 array([-1, 2]) >>> np.log(a) # 返回对数数组 array([ 1.09861229, 0.69314718, 1.38629436]) >>> np.exp(a) # 返回指数数组 array([ 20.08553692, 7.3890561 , 54.59815003]) >>> np.sqrt(a) # 返回开方数组 array([ 1.73205081, 1.41421356, 2. ]) >>> np.msort(a) # 数组排序 array([2, 3, 4]) >>> a = np.array([1,4,7]) >>> b = np.array([8,5,2]) >>> np.maximum(a, b) # 返回多个数组中对应位置元素的最大值数组 array([8, 5, 7]) >>> np.minimum(a, b) # 返回多个数组中对应位置元素的最小值数组 array([1, 4, 2]) >>> np.true_divide(a, b) # 对整数实现真正的数学除法运算 array([ 0.125, 0.8 , 3.5 ])
二、矩阵对象
matrix是矩阵对象,继承自ndarray类型,因此含有ndarray的所有数据属性和方法。不过,当你把矩阵对象当数组操作时,需要注意以下几点:
matrix对象总是二维的,即使是展平(ravel函数)操作或是成员选择,返回值也是二维的
matrix对象和ndarray对象混合的运算总是返回matrix对象
1、创建矩阵
matrix对象可以使用一个Matlab风格的字符串来创建(以空格分隔列,以分号分隔行的字符串),也可以用数组来创建。
>>> np.mat('1 4 7; 2 5 8; 3 6 9')
matrix([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]])
>>> np.mat(np.arange(1,10).reshape(3,3))
matrix([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
2、矩阵的特有属性
矩阵有几个特有的属性使得计算更加容易,这些属性有:
>>> m = np.mat(np.arange(1,10).reshape(3,3)) >>> m matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> m.T # 返回自身的转置 matrix([[1, 4, 7], [2, 5, 8], [3, 6, 9]]) >>> m.H # 返回自身的共轭转置 matrix([[1, 4, 7], [2, 5, 8], [3, 6, 9]]) >>> m.I # 返回自身的逆矩阵 matrix([[ -4.50359963e+15, 9.00719925e+15, -4.50359963e+15], [ 9.00719925e+15, -1.80143985e+16, 9.00719925e+15], [ -4.50359963e+15, 9.00719925e+15, -4.50359963e+15]]) >>> m.A # 返回自身数据的二维数组的一个视图 array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
3、矩阵乘法
对ndarray对象而言,星号是按元素相乘,dot()函数则当作矩阵相乘。对于matrix对象来说,星号和dot()函数都是矩阵相乘。特别的,对于一维数组,dot()函数实现的是向量点乘(结果是标量),但星号实现的却不是差乘。
>>> a = np.array([1,2,3]) >>> b = np.array([4,5,6]) >>> a*b # 一维数组,元素相乘 array([ 4, 10, 18]) >>> np.dot(a,b) # 一维数组,元素相乘再求和 32 >>> a = np.array([[1,2],[3,4]]) >>> b = np.array([[5,6],[7,8]]) >>> a*b # 多维数组,元素相乘 array([[ 5, 12], [21, 32]]) >>> np.dot(a,b) # 多维数组,实现的是矩阵相乘 array([[19, 22], [43, 50]]) >>> m = np.mat(a) >>> n = np.mat(b) >>> np.dot(m,n) # 矩阵相乘 matrix([[19, 22], [43, 50]]) >>> m*n # 矩阵相乘 matrix([[19, 22], [43, 50]])
三、线性代数模块
numpy.linalg 是numpy的线性代数模块,可以用来解决逆矩阵、特征值、线性方程组以及行列式等问题。
1、计算逆矩阵
尽管matrix对象本身有逆矩阵的属性,但用numpy.linalg模块求解矩阵的逆,也是非常简单的。
m = np.mat('0 1 2; 1 0 3; 4 -3 8')
mi = np.linalg.inv(m) # mi即为m的逆矩阵。何以证明?
m * mi # 矩阵与其逆矩阵相乘,结果为单位矩阵
matrix([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
2、计算行列式
如何计算行列式,我早已经不记得了,但手工计算行列式的痛苦,我依然记忆犹新。现在好了,你在手机上都可以用numpy轻松搞定(前提是你的手机上安装了python + numpy)。
m = np.mat('0 1 2; 1 0 3; 4 -3 8')
np.linalg.det(m) # 什么?这就成了?
2.0
3、计算特征值和特征向量
m = np.mat('0 1 2; 1 0 3; 4 -3 8')
>>> np.linalg.eigvals(m) # 计算特征值
array([ 7.96850246, -0.48548592, 0.51698346])
>>> np.linalg.eig(m) # 返回特征值及其对应特征向量的元组
(array([ 7.96850246, -0.48548592, 0.51698346]), matrix([[ 0.26955165, 0.90772191, -0.74373492],
[ 0.36874217, 0.24316331, -0.65468206],
[ 0.88959042, -0.34192476, 0.13509171]]))
4、求解线性方程组
有线性方程组如下:
x - 2y + z = 0 2y -8z = 8 -4x + 5y + 9z = -9
求解过程如下:
>>> A = np.mat('1 -2 1; 0 2 -8; -4 5 9')
>>> b = np.array([0, 8, -9])
>>> np.linalg.solve(A, b)
array([ 29., 16., 3.]) # x = 29, y = 16, z = 3
云海天教程网,大量的免费python教程,欢迎在线学习!
相关推荐:
1、Python数学建模三剑客之Matplotlib
2、Python数学建模三剑客之Scipy
来源:PY学习网:原文地址:https://www.py.cn/article.html

