前缀和与二维前缀和

前缀和

　　前缀和，顾名思义，就是所有前缀之和，给一个最基本的例子：

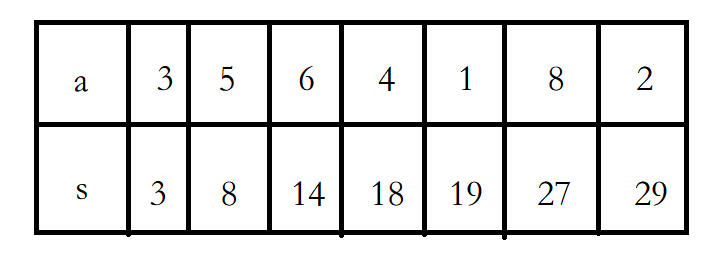
　　如图，a为原始数组，s为完成预处理后的数组，很容易看出来s[ i ]=s[ i – 1 ]+a[ i ]，而也就是s[ i ]=a[1]+a[2]+……+a[ i ]，需要注意的是记s[0]=0。

　　那么，如果我想要知道一个区间的区间和该怎么做呢？其实很简单，例如要求区间3~5的区间和，就可以用s[5]-s[2]=19-8=11。这里同样需要注意当减去区间左边界时需要将其减1，及求l~r的区间和，是用s[ r ]-s[ l-1 ]。

　　根据以上求区间前缀和的思路可以完成以下代码

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define MAXN 100010
 4 int n,m;
 5 int a[MAXN],s[MAXN];
 6 int main()
 7 {
 8     cin>>n; //数组的长度 
 9     for(int i=1;i<=n;i++)
10     {
11         cin>>a[i];  
12         s[i]=s[i-1]+a[i]; //这里就是上面讲到的预处理的方法 
13     }
14     cin>>m; //读入区间数量 
15     for(int i=1;i<=m;i++)
16     {
17         int l,r;
18         cin>>l>>r; //读入区间的左边界和右边界 
19         cout<<s[r]-s[l-1]<<endl; //输出区间和 
20     }
21     return 0;
22 }