P2448 无尽的生命

题目传送门

题意简述

看到题目显而易见是求逆序对个数。

思路分析

看到数据范围 (x_i,y_i le 2^{31}-1)，(k le 10^5)。数据值域大但是个数少，且与数据之间的大小关系有关，因此考虑离散化。

离散化简单介绍

离散化实际就是一种映射，当数据值域过大而个数有限时，可以尝试离散化。

具体过程以此题为例。假设给出这么一组数据

2

123456789 123456

987654321 123456

首先将所有出现过的数收集起来，存进 (a) 数组，并进行排序，然后再去重保存进 (pos) 数组当中。

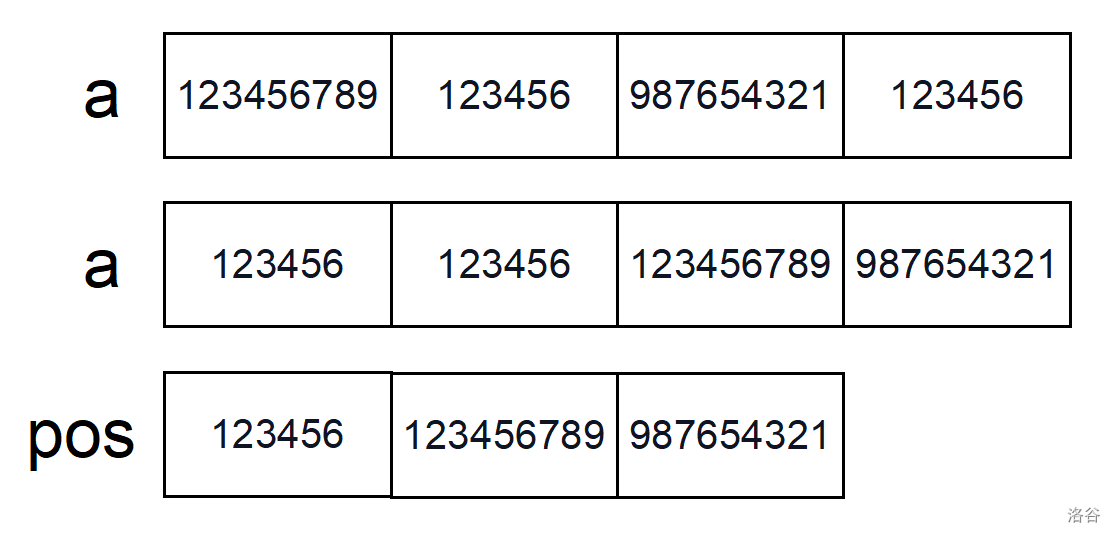
接下来就可以建立映射关系。将数值大的数在 (num) 数组中用数值小的数代替，但各个数之间的大小关系不变，接下来交换操作先用二分答案在 (pos) 数组中检索，然后通过映射在 (num) 数组中进行交换。

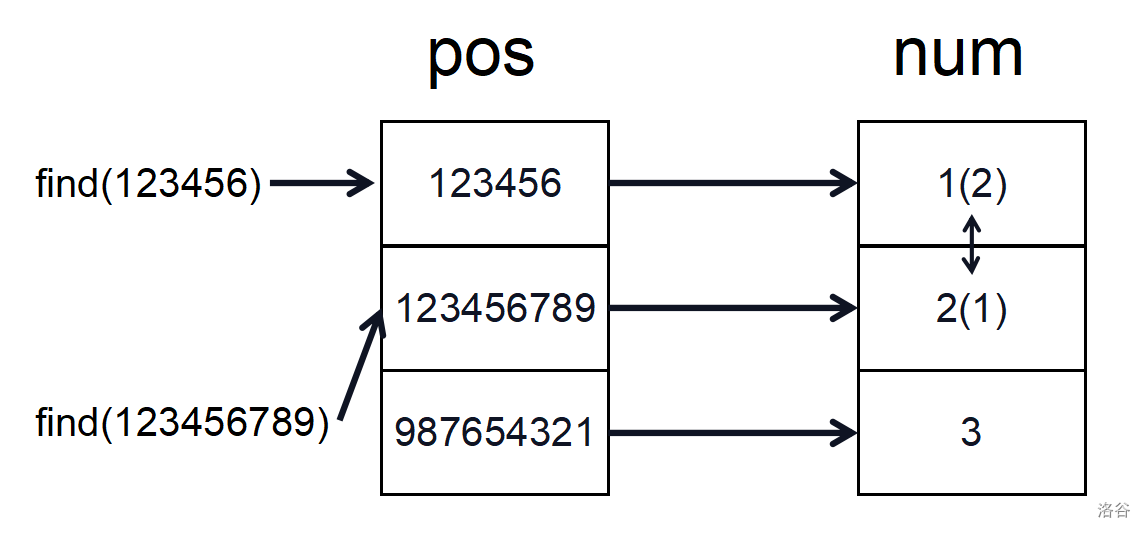
最终被交换过的数之间的逆序对在 (num) 数组中求即可。

被交换的数与未被交换的数之间的逆序对

考虑每个被交换的数对答案的贡献。

设 (x<y),当 (x) 和 (y) 交换后。

对于 (x) 来说, (x sim y) 之间所有未被交换的数都比 (x) 大，形成逆序对。

对于 (y) 来说，(x sim y) 之间所有未被交换的数都比 (y) 小，形成逆序对。

逆序对个数都为(x sim y) 之间所有未被交换的数。

温馨提示：以下主要为代码实现讲解，本质思想同上。

对于交换过后的 (num) 数组，(num_i) 表示的是位置 (pos_i) 上当前所在的数在 (num) 数组中对应的数。记数 (x) 为位置 (pos_i) 上当前所在的数。

(pos_{num_i}) 表示数 (x) 现在所在的位置。

(pos_i) 表示数 (x) 原来在的位置。

(leftvert pos_i-pos_{num_i}-1ightvert) 表示两个位置间所有的数。

(leftvert num_i-i-1ightvert) 表示两个位置间所有被交换过的数。

因此所有未被交换的数就为 (leftvert pos_i-pos_{num_i}-1ightvert – leftvert num_i-i-1ightvert)。

code

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
struct A{
	int x,y;
}a[100005];
int k,pos[200005],num[200005],cnt,len;
int t[100005];
void add(int x){
	for(;x<=len;x+=(x&-x)) t[x]+=1;
}
long long sum(int x){
	long long ans=0;
	for(;x;x-=(x&-x)) ans+=t[x];
	return ans;
}
int find(int x){
	int l=1,r=len;
	while(l<r){
		int mid=(l+r)>>1;
		if(pos[mid]<x) l=mid+1;
		else if(pos[mid]>x) r=mid-1;
		else return mid;
	}
} 
int main(){
	scanf("%d",&k);
	for(int i=1;i<=k;i++){
		scanf("%d%d",&a[i].x,&a[i].y);
		num[++cnt]=a[i].x;
		num[++cnt]=a[i].y;
	}
	sort(num+1,num+cnt+1);
	for(int i=1;i<=cnt;i++){
		if(num[i]==num[i-1]) continue;
		pos[++len]=num[i];
	}
	for(int i=1;i<=len;i++) num[i]=i;
	for(int i=1;i<=k;i++){
		int pos1=find(a[i].x);
		int pos2=find(a[i].y);
		swap(num[pos1],num[pos2]);
	}
	long long ans=0;
	for(int i=len;i>=1;i--){
		add(num[i]);
		ans+=sum(num[i]-1);
		ans+=abs(pos[num[i]]-pos[i]-1)-abs(num[i]-i-1); 
	} 
	cout<<ans<<endl;
	return 0;
}