高精度HighAccuracy_acwing.cpp

​​

​

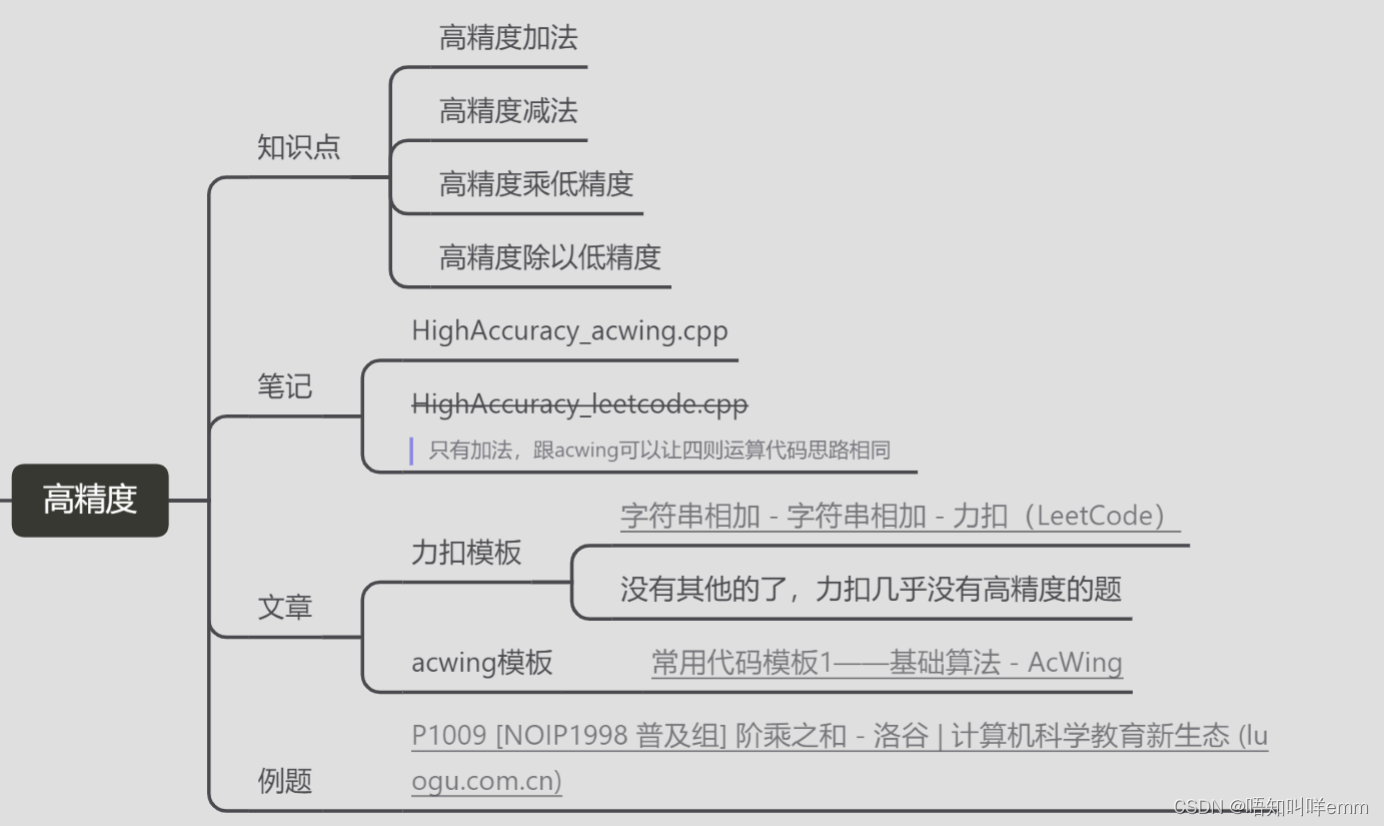
 文章：

        力扣模板：字符串相加 – 字符串相加 – 力扣（LeetCode）

        acwing模板：常用代码模板1——基础算法 – AcWing

例题：

        P1009 [NOIP1998 普及组] 阶乘之和 – 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

笔记：HighAccuracy_acwing.cpp

        说明：参考acwing的模板，但是和acwing模板不完全相同

​

#include<bits/stdc++.h>
using namespace std;

//HighAccuracy_acwing.cpp

/*
说明：
参考acwing的模板：https://www.acwing.com/blog/content/277/
但是和acwing模板不完全相同
*/

// C = A + B, A >= 0, B >= 0
//这里不加&，就可以避免改变了原来的a，b数组，使得a，b数组可以重复利用
vector<int> add(vector<int> A, vector<int> B){  //正序输入两个vector类型的“数”
    if (A.size() < B.size()) return add(B, A);  //使得A数组是最大的
    //如果未反转，在if下面加reverse，不能在if上面加reverse，否者二次反转，等于没有反转
    
    reverse(A.begin(),A.end());  //反转数组,变成个十百千万···
    reverse(B.begin(),B.end());
    vector<int> C;  //初始化答案数组
    int t = 0;
    for (int i = 0; i < A.size(); i ++ ){
        t += A[i];
        if (i < B.size()) t += B[i];  //如果B还有数字
        C.push_back(t % 10);
        t /= 10;
    }
    if (t) C.push_back(t);//最后一次加法可能还有进位的数，把最高位补上
    return C;
}

string add(string a, string b){
    if(a.size()<b.size()) return add(b,a);
    reverse(a.begin(),a.end());
    reverse(b.begin(),b.end());
    int t = 0;
    string c;
    for(int i = 0; i<a.size(); i++){
        t += a[i] - "0";
        if(i<b.size()) t+=b[i] - "0";
        c.push_back(t%10 + "0");
        t /= 10;
    }
    if(t) c.push_back(t + "0");
    reverse(c.begin(), c.end());
    return c;
}

// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> A, vector<int> B){
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ )    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

/*高精度乘低精度 —— 模板题*/
// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> A, int b){  //输入正序的高精度A和低精度b
    vector<int> C;  //初始化答案数组
    reverse(A.begin(),A.end());  //反转数组,变成个十百千万···
    int t = 0;
    for (int i = 0; i < A.size() || t; i++ ){  //A数组还有数 或 t还有数
        if (i < A.size()) t += A[i] * b;  //如果 A数组还有数
        C.push_back(t % 10);
        t /= 10;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();  //末尾可能是0，都要去掉（我感觉是多余的，不可能有这种情况）(难道是处理b==0？)
    reverse(C.begin(),C.end());  //反转数组,恢复正序
    return C;
}

string mul(string a, int b){
    reverse(a.begin(), a.end());
    string c;
    int t = 0;
    for(int i = 0; i<a.size() || t; i++){
        if(i<a.size()) t += (a[i] - "0") * b;
        c.push_back(t%10 + "0");
        t /= 10;
    }
    while(c.size()>1 && c.back() == 0)c.pop_back();
    reverse(c.begin(), c.end());
    return c;
}

int main(){
    //加法
    vector<int> addint1 = {1,2,3,4,5,6,7,8,9};
    vector<int> addint2 = {9,8,7,6,5,4,3,2,1,0};
    vector<int> addint3 = add(addint1,addint2);
    for(int i = 0;i<addint3.size(); i++) cout<<addint3[i];
    printf("
");

    //加法
    string addstr1 = {"123456789"};
    string addstr2 = {"9876543210"};
    string addstr3 = add(addstr1,addstr2);
    cout<< addstr3 <<endl;

    //乘法
    vector<int> mulint1 = {1,2,3,4,5,6,7,8,9};
    int mulint2 = 100000;
    vector<int> mulint3 = mul(mulint1,mulint2);
    for(int i = 0;i<mulint3.size(); i++) cout<<mulint3[i];
    printf("
");

    //乘法
    string mulstr1 = "123456789";
    int mulstr2 = 100000;
    cout<<mul(mulstr1,mulstr2)<<endl;

    return 0;
}