LRU：最近最少使用缓存

LRU是Least Recently Used的缩写，即最近最少使用，是一种常用的页面置换算法，选择最近最久未使用的页面予以淘汰。该算法赋予每个页面一个访问字段，用来记录一个页面自上次被访问以来所经历的时间 t，当须淘汰一个页面时，选择现有页面中其 t 值最大的，即最近最少使用的页面予以淘汰。（引自百度百科）

运用所掌握的数据结构，设计和实现一个 LRU (Least Recently Used，最近最少使用) 缓存机制 。

实现 LRUCache 类：

• LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
• int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
• void put(int key, int value) 如果关键字已经存在，则变更其数据值；如果关键字不存在，则插入该组「关键字-值」。当缓存容量达到上限时，它应该在写入新数据之前删除最久未使用的数据值，从而为新的数据值留出空间。

解题思路

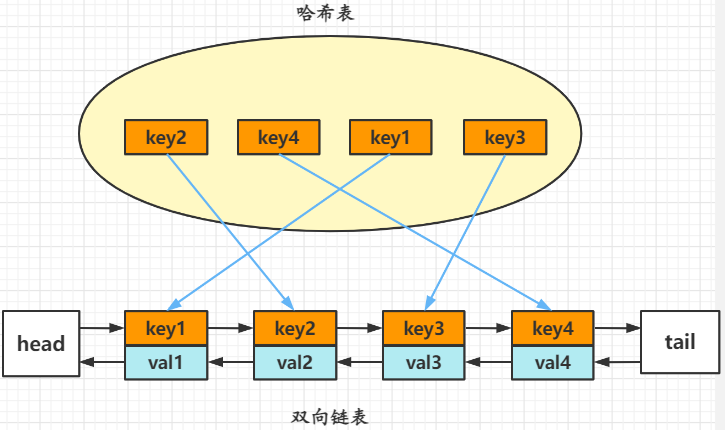
LRU缓存机制对应的结构其实就是一个双向链表，由于get和put方法必须是(O(1))的时间复杂度，可以使用一个哈希表快速定位，找出缓存项在双向链表中的位置，随后将其移动到双向链表的头部（最近使用的排在队头，最久未使用的排在队尾），即可在 (O(1)) 的时间内完成 get 或者 put 操作。

因此，LRU 算法的核心数据结构就是哈希链表，即双向链表和哈希表的结合体。

对于get操作，首先在哈希map中判断key是否存在：

• 如果key不存在，直接返回-1；
• 如果key存在，则 key 对应的节点就是最近被使用的节点。通过哈希表定位到该节点在双向链表中的位置，并将其移动到双向链表的头部，最后返回该节点的值。

对于put操作，首先也要在哈希 map 中判断 key 是否存在：

• 如果 key 不存在，使用 key 和 value 创建一个新的节点，在双向链表的头部添加该节点，并将 key 和该节点添加进哈希表中。然后判断双向链表是否满了，如果超出了容量，则删除双向链表的尾部节点（把最久未使用的尾部结点给删了，给新节点腾地儿），并删除哈希表中对应的键值。最后把新加入的key添加到双向链表的头部和哈希表中；
• 如果 key 存在，则与 get 操作类似，通过查询哈希表得到key在双向链表的位置，删除该结点。最后把新加入的key添加到双向链表的头部和哈希表中；

在双向链表初始化时，使用一个哑元头部（dummy head）和哑元尾部（dummy tail）标记占位，这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在，防止空指针。

代码实现

自定义双向链表结构（面试推荐✔）

class LRUCache {
    
    // 自定义结点类型
    static class Node {
        private int key, val;
        private Node next, prev;
        
        public Node(int k, int v) {
            this.key = k;
            this.val = v;
        }
    }
    
    // 自定义双向链表
    static class DoubleList {
        private Node head, tail;
        // 构造双向链表（head和tail是哑元结点，占位用的）
        public DoubleList() {
            this.head = new Node(-1, -1);
            this.tail = new Node(-1, -1);
            head.next = tail;
            tail.prev = head;
        }
        
        // 在链表头部添加结点（头插法）
        public void addFirst(Node node) {
            node.prev = head;
            node.next = head.next;
            head.next.prev = node;
            head.next = node;
        }
        
        // 删除指定结点Node
        public void remove(Node node) {
            node.prev.next = node.next;
            node.next.prev = node.prev;
        }
        
        // 删除链表尾节点，并返回该结点
        public Node removeLast() {
            Node node = tail.prev;
            remove(node);
            return node;
        }
    }
    
    private HashMap<Integer, Node> map;		// 辅助map
    private DoubleList cache;
    private int cap;	// 双向链表的最大容量

    public LRUCache(int capacity) {
		map = new HashMap<>();
        cache = new DoubleList();
        this.cap = capacity;
    }
    
    public int get(int key) {
		if(! map.containsKey(key))	return -1;	// map中不存在key，get不到了
        Node node = map.get(key);
        cache.remove(node);
        cache.addFirst(node);
        return node.val;
    }
    
    public void put(int key, int value) {
        // 要添加的结点封装成一个node
        Node node = new Node(key, value);
        if(map.containsKey(key)) {
            cache.remove(map.get(key));		// 已经有这个key了，旧值删了，新值头部添加操作在底下
        } else if(map.size() >= cap) {
            // 双端链表满了，则把最久未使用的尾部结点给删了，给新节点腾地儿
            Node lastNode = cache.removeLast();
            map.remove(lastNode.key);
        }
        // 链表和map同步添加
        cache.addFirst(node);
        map.put(key, node);
    }
    
    // 测试
    public static void main(String[] args) {
        LRUCache lruCache = new LRUCache(2);	// 初始化双向链表和map
        lruCache.put(1, 1);
        lruCache.put(2, 2);
        lruCache.get(1);
        lruCache.put(3, 3);
        lruCache.get(2);
        System.out.println(lruCache.map);
    }
}

在 Java 语言中，同样有类似的数据结构 LinkedHashMap，内部已经封装好添加查询的方法。但是面试时不推荐使用，还是推荐使用上面这种方式。

class LRUCache {

    private int cap;
    private LinkedHashMap<Integer, Integer> cache;

    public LRUCache(int capacity) {
        this.cap = capacity;
        this.cache = new LinkedHashMap<>()
    }

    // 使用了key，就得设这个key为最近使用
    public int get(int key) {
        if(! cache.containsKey(key)) {
            return -1;
        }
        makeRecently(key);
        return cache.get(key);
    }

    public void put(int key, int value) {
        // key 存在于链表中
        if(cache.containsKey(key)) {
            cache.put(key, value);    // 修改 key 的值
            makeRecently(key);      // 将 key 变为最近使用
            return;
        }
        // 插入元素前需要判断链表容量是否已满，淘汰最久未使用的key
        if(cache.size() >= this.cap) {
            // 链表头部就是最久未使用的 key
            int oldestKey = cache.keySet().iterator().next();
            cache.remove(oldestKey);
        }
        // 将新的 key 添加链表尾部
        cache.put(key, value);
    }

    // 设置key为最近使用，key先删了移到链表尾
    private void makeRecently(int key) {
        int val = cache.get(key);
        // 删除 key，重新插入到队尾
        cache.remove(key);
        cache.put(key, val);
    }

    // 测试
    public static void main(String[] args) {
        LRUCache lruCache = new LRUCache(2);
        lruCache.put(1,1);
        lruCache.put(2,2);
        lruCache.get(1);
        lruCache.put(3,3);
        lruCache.get(2);
        System.out.println(cache);
    }

}

复杂度

• 时间复杂度：put 和 get 操作的平均时间复杂度都为(O(1))；
• 空间复杂度：(O(capacity))，哈希表和双向链表中最多存储 capacity 个元素。

参考

labuladong：https://leetcode.cn/problems/lru-cache/solutions/12711/lru-ce-lue-xiang-jie-he-shi-xian-by-labuladong/