分治的理解
分治的理解
把规模为n的问题P(n),分解为k个规模较小、互相独立、结构与原来问题结构相同的子问题,又进一步的分解每个子问题,直到某个阀值n0为止。递归地解这些子问题,再把子问题的解合并起来,得到原问题的解。
divide-and-conquer(P)
{
if ( | P | <= n0) adhoc(P); //解决小规模的问题
divide P into smaller subinstances P1,P2,...,Pk;//分解问题
for (i=1,i<=k,i++)
yi=divide-and-conquer(Pi); //递归的解各子问题
return merge(y1,...,yk); //将各子问题的解合并为原问题的解
}
人们从大量实践中发现,在用分治法设计算法时,最好使子问题的规模大致相同。即将一个问题分成大小相等的k个子问题的处理方法是行之有效的。这种使子问题规模大致相等的做法是出自一种平衡(balancing)子问题的思想,它几乎总是比子问题规模不等的做法要好。
分治法设计步骤
三个步骤组成:
-
划分步:把输入的问题实例划分为k个子问题。尽量使k个子问题的规模大致相同。在很多情况下,使k=2。也有k=1的划分,仍把问题划分成两部分,取其中的一部分,而丢弃另一部分,如二叉检索问题用分治法处理 。
-
治理步:当问题的规模大于某个预定义的阀值n0时,治理步由k个递归调用组成。
阀值n0的选取:阀值可为任何正常数,大小与算法的性能有关。取决于算法中的adhoc对阀值n0的敏感程度,以及merge的处理情况。
-
组合步:把子问题的解组合起来,对分治算法的实际性能至关重要 。算法的有效性很大程度上依赖于组合步的实现!
分治法的复杂性分析
一个分治法将规模为n的问题分成k个规模为n/m的子问题去解。设分解阀值n0=1,且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间,则有:
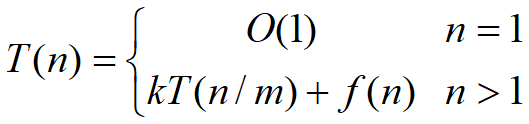
题目
给定数组a[0:n-1],试设计一个算法,在最坏情况下用┌ 3n/2-2 ┐次比较找出a[0:n-1]中元素的最大值和最小值。
-
算法思想
- 用分治法求最大值和次大值首先将问题划分,即将划分成长度相等的两个序列,递归求出 左边的最大值次大值,再求出右边的的最大值次大值,比较左右两边,最后得出问题的解。
-
复杂度分析:
-
把问题划分为左右两种的情况,需要分别递归求解,时间复杂度可如下计算:
-
有递推公式为:
-
- T(n)= 1 n=l - T(n)=2T(n/2)+l n>l -
所以,分治算法的时间复杂度是n+[logn]-2,当n为奇数时,logn取上线,当n为偶数时,logn取下线。
-
-
#include<stido.h> int a[100]; void maxcmax(int i,int j,int &max,int &cmax){ int lmax,lcmax,rmax,rcmax; int mid; if(i==j){ max=a[i]; cmax=a[i]; } else if(i==j-1){ if(a[i]<a[j]){ max=a[j]; cmax=a[i]; }else{ max=a[i]; cmax=a[j]; } }else{ mid = (i+j)/2; maxcmax(i,mid,lmax,lcmax); maxcmax(mid+1,j,rmax,rcmax); if(lmax>rmax){ if(lcmax>rmax){ max=lmax; cmax=lcmax; }else{ max=lmax; cmax=rmax; } }else{ if(rcmax>lmax){ if(rcmax==rcmax){ max=lmax; cmax=lcmax; }else{ max=lmax; cmax=rmax; } }else{ max=rmax; cmax=lmax; } } } }


