树基本概念及用法
1.树的基础知识概述
树状图是一种数据结构,它是由 n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
每个结点有零个或多个子结点;没有父结点的结点称为根结点;每一个非根结点有且只有一个父结点;除了根结点外,每个子结点可以分为多个不相交的子树;
| 专业术语 | 中 文 | 描 述 |
|
Root |
根节点 | 一棵树的顶点 |
| Child | 孩子节点 | 一个结点含有的子树的根结点称为该结点的子结点 |
| Leaf | 叶子节点 | 没有孩子的节点(度为0) |
| Degree | 度 | 一个节点包含的子树的数量 |
| Edge | 边 | 一个节点与另外一个节点的连接 |
| Depth | 深度 | 根节点到这个节点经过的边的数量 |
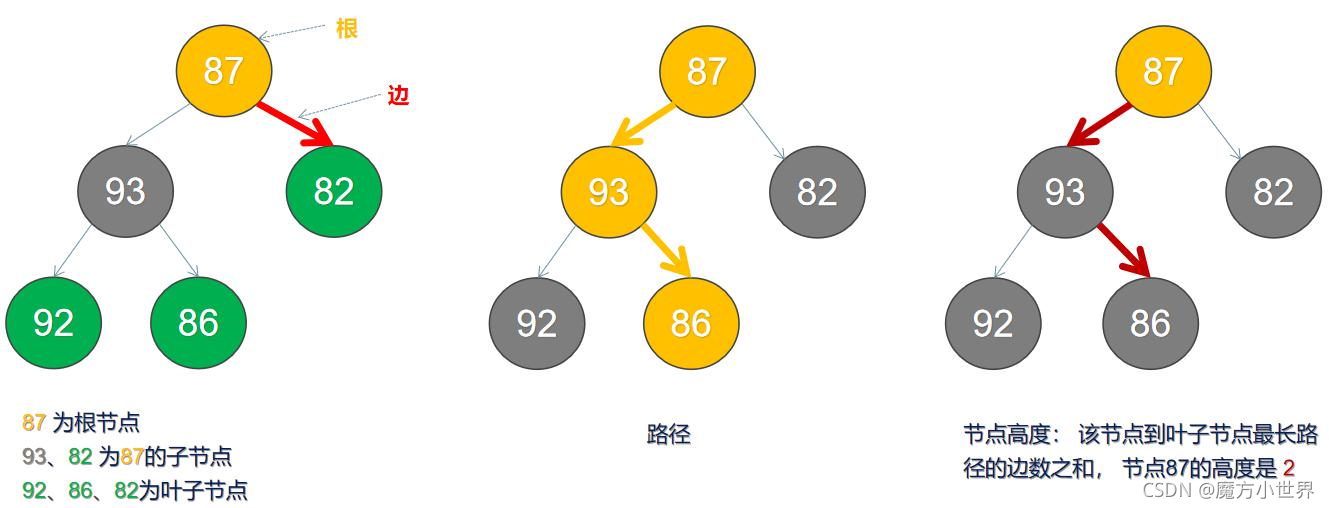
| Height | 节点高度 | 从当前节点到叶子节点形成路径中边的数量 |
| Level | 层级 | 节点到根节点最长路径的边的总和 |
| Path | 路径 |
一个节点和另一个节点之间经过的边和 Node 的序列 |

2.二叉树
2.1二叉树的基本概念
二叉树是n(n≥0)个结点的有限集合,该集合或者为空集(空二叉树),或者由一个根结点和两个互不相交的、分别称为根结点左子树和右子树的二叉树组成。
二叉树是一个每个结点最多只能有两个分支的树,左边的分支称之为左子树,右边的分支称之为右子树。
(1)在风控二叉树,第i-1层的结点总数不超过,i>=1; (2)深度为h-1的二叉树最多有-1个结点(h>=1),最少有h个结点 (3)对于任意一棵二叉树,如果叶节点为N0,而度数为2 的结点总数为N2,则N0=N2+1;
每个度为1的结点有1条边,度为2的结点有两条边。所以总边数为1*n1+2*n2,总边数等于结点数减1,即 N-1 = 1*n1+2*n2。其中总结点数又等于度为1、度为2、度为0的结点数和,即 N = n1 + n2 + n0;联立可得N0=N2+1。


