线段树

前置知识

二叉树

定义

基本操作复杂度： $ O(logn) $

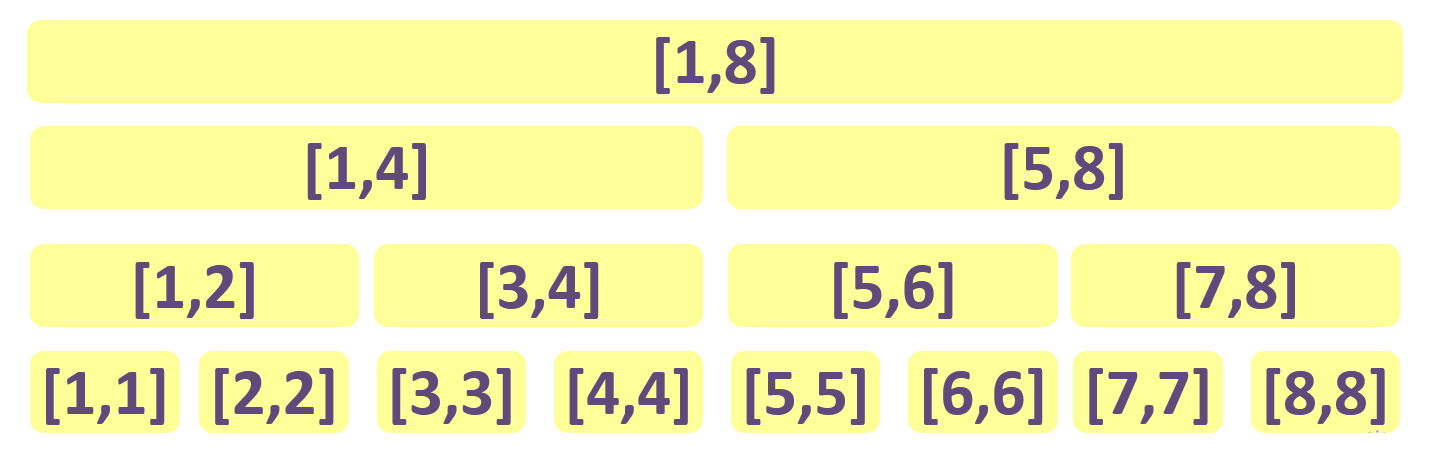
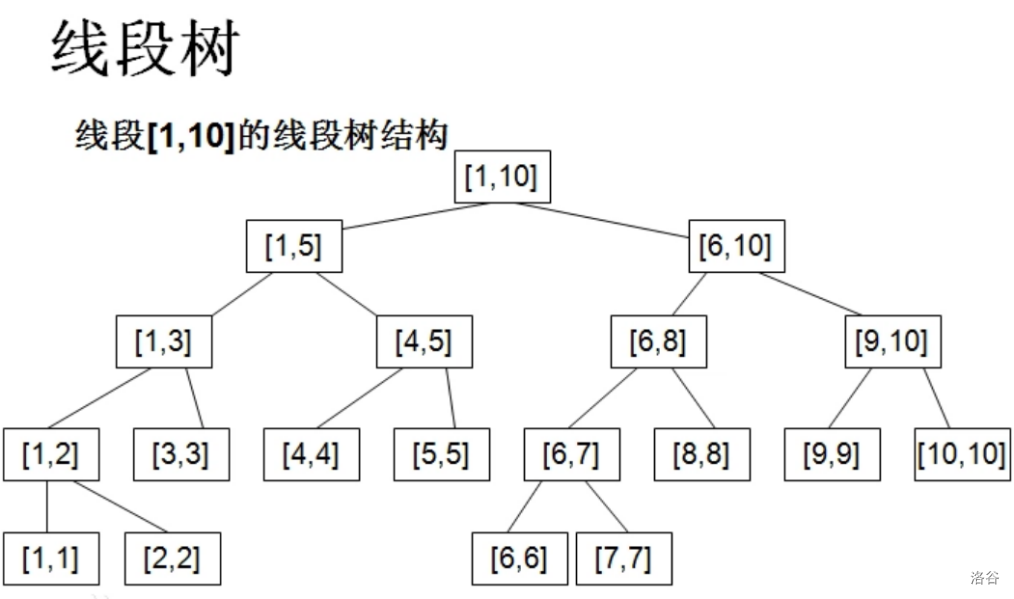
线段树是一棵二叉树，每个节点表示序列上的一段区间，其中根节点表示区间[1,n]。

从根节点开始，只要区间长度不为1，就将区间划分为两半，并分给两个子节点。

若当前节点表示区间[l,r]，

当l≠r时，左孩子表示[l,(l+r)/2]，右孩子表示[(l+r)/2+1,r]；

当l=r时，该节点为叶子节点。

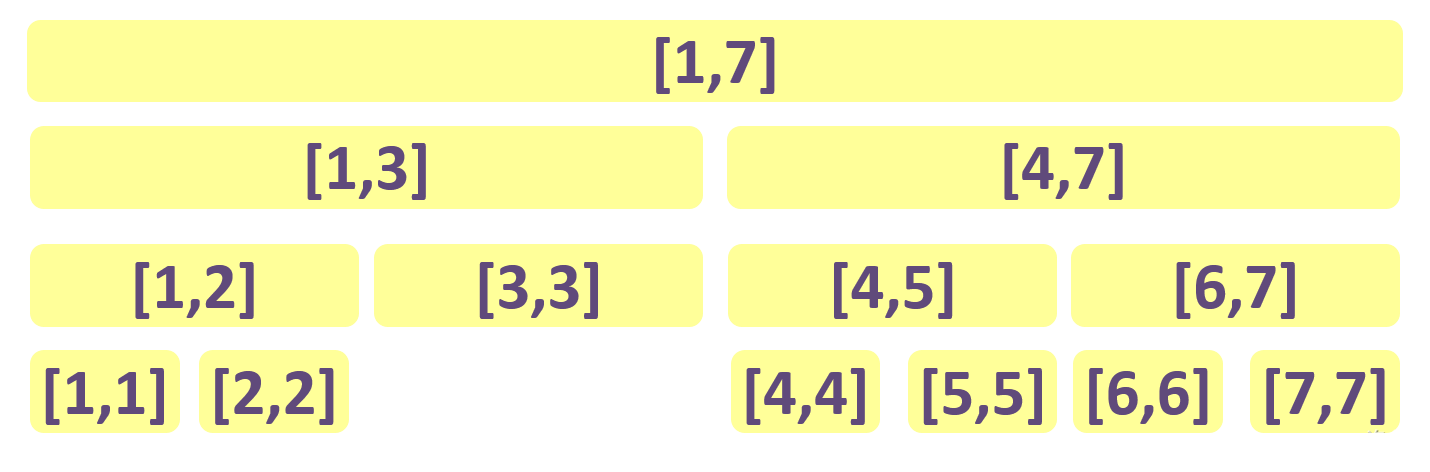
基本性质

性质1

线段树的总节点数为2n-1。

性质2

线段树的层数约为 $ log_{ 2 } n $ ，即每个叶节点到根节点的距离约为 (log_{2}n) 。

性质3

任何区间都可以用不超过 (2log_{2}n) 个节点组合而成。

编号

线段树的编号方式通常有两种：即2i和2i+1作i的孩子或按构建顺序编号。

存储

线段树的存储也有两种方式：多个数组或struct结构体。

以struct结构体数组为例:

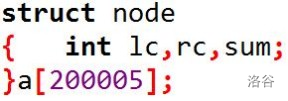
（lc,rc分别为左右孩子的编号，sum为该区间的总和。

数组大小为序列长度两倍。

至于区间的左右端点[l,r]，可以存储，也可以递归时计算。

若需要节省空间，则不存储。）

构建

构建过程递归实现，

void build(int u,int l,int r)

（u为当前节点编号，l,r为区间端点）

从根节点开始构建，递归时计算并代入l,r，若l=r，该点为叶子节点，令sum=序列原值，否则，递归构建左右孩子，之后令sum=sum左孩子+sum右孩子。

在主程序中：

t=1;

build(1,1,n);

即可。

应用

单点修改

修改过程递归实现，

void update(int u,int l,int r,int x,int w)

（u当前节点编号,l和r为区间端点，x为要修改的位置，w为变化量）

从根节点开始修改，若当前点为叶子节点，使sum+=w并返回
否则判断x在左孩子还是右孩子，递归进行修改，之后令sum=左孩子sum+右孩子sum。

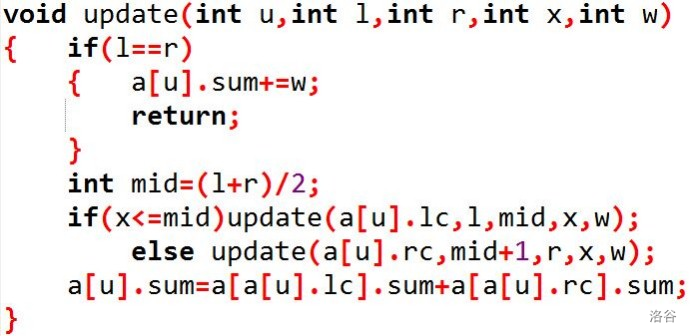
在主程序中调用：

update(1,1,n,x,y);

区间和查询

查询过程递归实现，

void query(int u,int l,int r,int ll,int rr)

（u为当前节点，l和r是区间端点，ll和rr分别为所查询区间的左右端点）

需要用外层定义变量ans储存答案。

从根节点开始，首先判断查询区间与节点区间是否完全重合，若重合，ans+=sum并返回，否则判断查询区间是否完全在左孩子或者右孩子，若是则递归查询。否则将查询区间拆分，两侧分别递归查询。

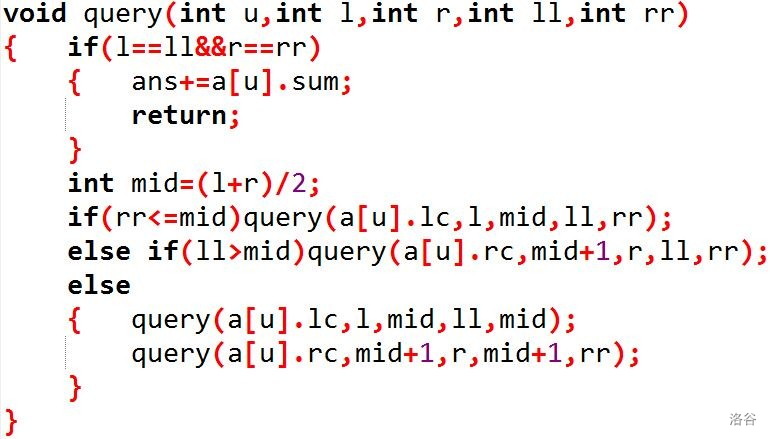
在主程序中：

ans=0;

query(1,1,n,x,y);

维护区间最大值/最小值

区间修改

我们在线段树的每个节点上再储存一个信息，称为“标记”，记为tag，表示该节点所包含的每个位置，都要再加上tag。

首先，像区间询问一样将区间对应到尽量少的节点上，

令它们

	sum+=(r-l+1)*w;//增加的区间和
	tag+=w;//增加标记 

然后将sum信息向上pushup。

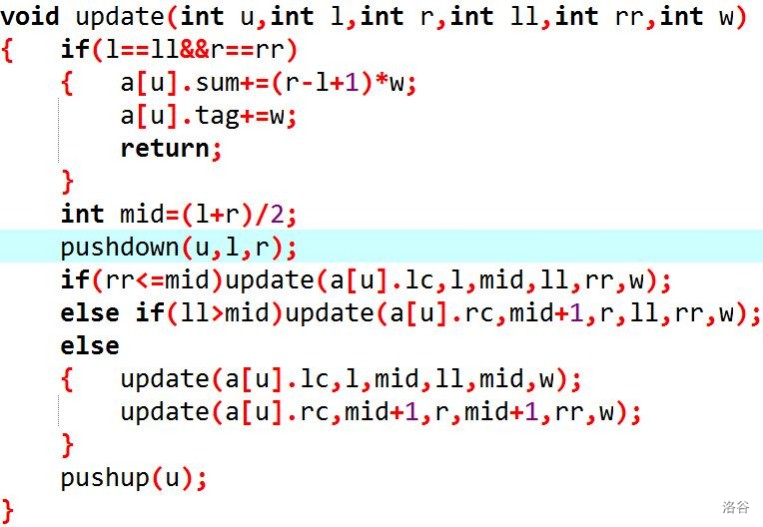
区间修改后的单点/区间查询

查询与之前类似，

查询过程递归实现，

void query(int u,int l,int r,int ll,int rr,int w)

但由于标记的出现，多了“下传标记”一步。

下传标记时，孩子的标记要叠加。

类似于pushup，标记下传的过程写入一个

void pushdown(int u,int l,int r)

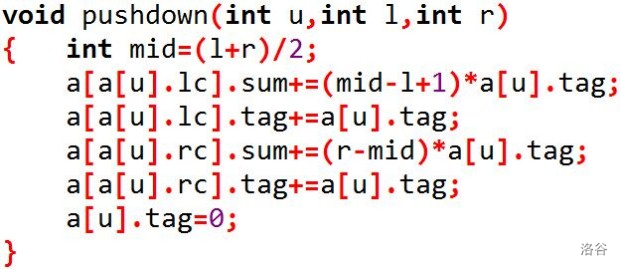
注

一个节点上的tag一定已经计入自身的sum。

在修改和查询时，只要需要进入子节点，就一定要pushdown。

注意

当维护信息较多时，为简化代码，通常将类似于”a[u].sum=a[a[u].lc].sum+a[a[u].rc].sum”的上传信息的步骤写入void pushup(int u)并调用pushup(u);

并非原创，仅是整理，请见谅